Question

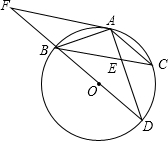如图，BD为⊙O的直径，AB=AC，AD交BC于点E，AE=1，ED=2．
（1）求证：∠ABC=∠D；
（2）求AB的长；
（3）延长DB到F，使得BF=BO，连接FA，试判断直线FA与⊙O的位置关系，并说明理由．

Answer 1

考点：切线的判定,圆周角定理,相似三角形的判定与性质

专题：

分析：（1）由AB=AC，利用等边对等角得到∠ABC=∠C，再由同弧所对的圆周角相等得到∠C=∠D，等量代换即可得证；
（2）由（1）的结论与公共角相等，得到△ABE与△ADB相似，由相似得比例，即可求出AB的长；
（3）直线FA与⊙O相切，理由为：连接OA，由BD为直径，得到∠BAD为直角，在Rt△ABD中，利用勾股定理求出BD的长，得到AB=OB=OA，根据BF=BO，得到AB等于FO的一半，确定出∠OAF为直角，即可得证．

解答：（1）证明：∵AB=AC，
∴∠ABC=∠C，
∵∠C与∠D所对应的弧均为

AB

，
∴∠C=∠D，
∴∠ABC=∠D；

（2）解：∵∠ABC=∠D，∠BAE=∠DAB，
∴△ABE∽△ADB，
∴

AB

AD

=

AE

AB

，
即AB²=AE•（AE+ED）=3，
解得：AB=

3

；

（3）答：直线FA与⊙O相切．理由如下：
连接OA，
∵BD为⊙O的直径，
∴∠BAD=90°，
在Rt△ABD中，AB=

3

，AD=1+2=3，
根据勾股定理得：BD=2

3

，
∴OB=OA=AB=

3

，
∵BF=OB，
∴AB=FB=OB，即AB=

1

2

OF，
∴∠OAF=90°，
则直线AF与⊙O相切．

点评：此题考查了切线的判定，圆周角定理，以及相似三角形的判定与性质，熟练掌握切线的判定方法是解本题的关键．