题目内容

已知数a，b在数轴上的位置如图，化简
(a+b)2
-
a(a-b)
|a-b|
．
考点：二次根式的性质与化简,实数与数轴
专题：
分析：根据数轴得出a＜-1＜0＜b＜1，求出原式=-a-b-
a(a-b)
-(a-b)
，去掉绝对值符号后合并即可．
解答：解：∵从数轴可知：a＜-1＜0＜b＜1，
∴
(a+b)2
-
a(a-b)
|a-b|

=-a-b-
a(a-b)
-(a-b)

=-a-b+a
=-b．
点评：本题考查了绝对值，数轴，二次根式的性质的应用，解此题的关键是能正确根据绝对值和二次根式的性质得出-a-b-
a(a-b)
-(a-b)
，题目比较好，难度适中．
练习册系列答案
相关题目
在下列说法中是错误的（　　）
A、若∠C=∠A一∠B，则△ABC为直角三角形
B、若a：b：c=2：2：2
2
，则△ABC为直角三角形
C、若a=
3
5
c，b=
4
5
c，则△ABC为直角三角形
D、若∠A：∠B：∠C=3：4：5，则△ABC为直角三角形
如图，△ABC的两条高分别为BE、CF，M为BC的中点．求证：ME=MF．
甲、乙两人同解方程组
ax+5y=15  (1)
4x=by-2     (2)
时，甲看错了方程（1）中的a，解得
x=2
y=1
，乙看错（2）中的b，解得
x=5
y=4
．试求a、b的值．
如图，AB为⊙O的直径，AB=4，P为AB上一点，过点P作⊙O的弦CD，设∠BCD=m∠ACD．
（1）已知
1
m
=
2
m+2
，求m的值，及∠BCD、∠ACD的度数各是多少？
（2）当
AP
PB
=
2-
3
2+
3
时，是否存在正实数m，使弦CD最短？如果存在，求出m的值，如果不存在，说明理由；
（3）在（1）的条件下，且
AP
PB
=
1
2
，求弦CD的长．
（1）请你任意写5个正的真分数：
 
、
 
、
 
、
 
、
 
．给每个分数的分子分母同时加上同一个正数得到5个新的分数：
 
、
 
、
 
、
 
、
 
．
（2）比较原来的每个分数与对应新分数的大小，可以得到下面的结论：
一个真分数
a
b
（a、b均为正数），给其分子、分母同时加上一个正数m，得
a+m
b+m
，则两个分数的大小关系是：
a+m
b+m
 
a
b
；
（3）利用（2）中的结论，解决下面的问题：
如图，有一个长宽不等的长方形绿地，现在绿地四周铺一条宽度相等的小路，问原来的长方形与铺过小路后的长方形是否相似？为什么？
 
．
已知一个三角形的三边长分别是7厘米，3厘米，第三边长为x厘米．
（1）求第三边x的取值范围；
（2）在（1）的条件下，取x的偶数值为直角△ABC的两直角边长（AC＞BC），此时AB=10厘米，若P为斜边AB上的一个动点，求PC的最小值．
如图所示，已知AB=AC，CB平分∠ACD，证明：AB∥CD．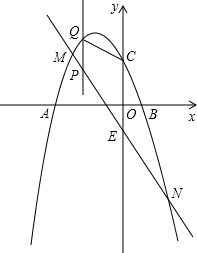
如图，抛物线y=-x2+bx+c交x轴于点A、B，交y轴于点C，其中点B坐标为（1，0），点C坐标为（0，3）．
（1）求抛物线的解析式；
（2）设直线y=kx-1（k≠0）与抛物线交于点M、N，试求出当y轴平分△CMN的面积时的直线函数关系式；
（3）在（2）的条件下，设直线y=kx-1与y轴相交于点E，点P是直线y=kx-1上一点，过点P作直线PQ平行于y轴yOx交抛物线于点Q，连接CQ，问是否存在以P、E、C、Q为顶点的四边形是平行四边形？若存在求出点P的坐标；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网