题目内容
7. 用三根长度分别为80cm,60cm,60cm的木条做成一个等腰三角形(如图),这个等腰三角形各个内角的大小分别为多少(精确到1″)?
用三根长度分别为80cm,60cm,60cm的木条做成一个等腰三角形(如图),这个等腰三角形各个内角的大小分别为多少(精确到1″)?
分析 如图,AB=AC=60cm,BC=80cm,作AD⊥BC于D,根据等腰三角形的性质得∠B=∠C,BD=CD=$\frac{1}{2}$BC=40,在Rt△ABD中,计算出cosB=$\frac{2}{3}$,则可得到∠B=41°48′54″,于是得到∠C的度数,然后根据三角形内角和定理计算∠BAC的度数.
解答 解:如图,AB=AC=60cm,BC=80cm,作AD⊥BC于D,
∵AB=AC,AD⊥BC,
∴∠B=∠C,BD=CD=$\frac{1}{2}$BC=40,
在Rt△ABD中,∵cosB=$\frac{BD}{AB}$=$\frac{40}{60}$=$\frac{2}{3}$,
∴∠B=41°48′54″,
∴∠C=41°48′54″,
∴∠BAC=180°-2∠B=96°22′12″.
即三角形三个内角的度数分别为41°48′54″,41°48′54″,96°22′12″.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.解决本题的关键的灵活运用勾股定理和锐角三角函数的定义.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
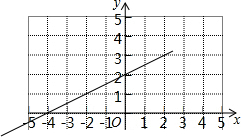 如图是某一次函数的图象,请根据图象回答问题;
如图是某一次函数的图象,请根据图象回答问题;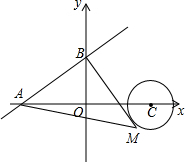 如图,已知直线y=$\frac{3}{4}$x+3与坐标轴分别交于A、B两点,M是以C(6,0)为圆心,2为半径的圆上一动点,连结MA、MB,则△MAB面积的最大值是20.
如图,已知直线y=$\frac{3}{4}$x+3与坐标轴分别交于A、B两点,M是以C(6,0)为圆心,2为半径的圆上一动点,连结MA、MB,则△MAB面积的最大值是20.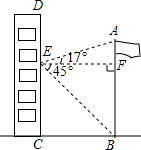 如图,在某次数学活动课中,小明为了测量校园内旗杆AB的高度,站在教学楼CD上的E处测得旗杆底端B的仰角∠BEF的度数为45°,测得旗杆顶端A的仰角∠AEF的度数为17°,旗杆底部B处与教学楼底部C处的水平距离BC为9m,求旗杆的高度(结果精确到0.1m).
如图,在某次数学活动课中,小明为了测量校园内旗杆AB的高度,站在教学楼CD上的E处测得旗杆底端B的仰角∠BEF的度数为45°,测得旗杆顶端A的仰角∠AEF的度数为17°,旗杆底部B处与教学楼底部C处的水平距离BC为9m,求旗杆的高度(结果精确到0.1m).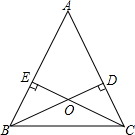 如图,锐角△ABC中AB=c,AC=b,BC=a且有b2-c2=ac-ab.
如图,锐角△ABC中AB=c,AC=b,BC=a且有b2-c2=ac-ab.