题目内容
18.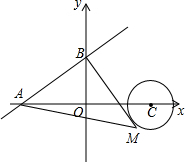 如图,已知直线y=$\frac{3}{4}$x+3与坐标轴分别交于A、B两点,M是以C(6,0)为圆心,2为半径的圆上一动点,连结MA、MB,则△MAB面积的最大值是20.
如图,已知直线y=$\frac{3}{4}$x+3与坐标轴分别交于A、B两点,M是以C(6,0)为圆心,2为半径的圆上一动点,连结MA、MB,则△MAB面积的最大值是20.
分析 过点C作CD⊥AB垂足为D,延长DC交圆C与点M,令x=0可求得点B的坐标,令y=0可求得点A的坐标,然后利用勾股定理可求得AB=5,然后证明△ABO∽△ACD,由相似三角形的性质可求得DC=6,从而得到DM=8,最后利用三角形的面积公式求解即可.
解答 解:如图所示:过点C作CD⊥AB垂足为D,延长DC交圆C与点M.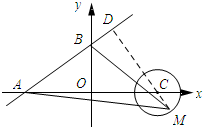
∵将x=0代入y=$\frac{3}{4}$x+3得;y=3,
∴点B的坐标为(0,3).
∴OB=3.
∵将y=0代入y=$\frac{3}{4}$x+3得;$\frac{3}{4}x+3$=0,解得:x=-4.
∴点A的坐标为(-4,0).
∴OA=4.
在Rt△ABO中,AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5.
∵点C的坐标为(6,0),
∴AC=10.
∵CD⊥AB,
∴∠CDA=∠AOB=90°.
又∵∠DAC=∠BAO,
∴△ABO∽△ACD.
∴$\frac{AB}{AC}=\frac{OB}{DC}$,即$\frac{5}{10}=\frac{3}{DC}$.
解得:DC=6.
∵圆C的半径为2,
∴MD=6+2=8.
∴${S}_{△ABM}=\frac{1}{2}AB•DM$=$\frac{1}{2}×5×8$=20.
故答案为:20.
点评 本题主要考查的是相似三角形的性质和判定、勾股定理、一次函数的图象和性质,掌握本题辅助线的作法是解题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
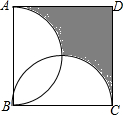 如图,正方形ABCD的边长为2,分别以AB、BC为直径,在正方形内作半圆,则图中阴影部分的面积为(3-$\frac{π}{2}$)平方单位.
如图,正方形ABCD的边长为2,分别以AB、BC为直径,在正方形内作半圆,则图中阴影部分的面积为(3-$\frac{π}{2}$)平方单位. 如图所示,在Rt△ABC中,BC=7.85,AB=11.40,解这个直角三角形.(边长保留三个有效数字,角度精确到1°)
如图所示,在Rt△ABC中,BC=7.85,AB=11.40,解这个直角三角形.(边长保留三个有效数字,角度精确到1°)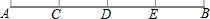 如图,点C、D、E在线段AB上,且AC=CD=DE=EB
如图,点C、D、E在线段AB上,且AC=CD=DE=EB 用三根长度分别为80cm,60cm,60cm的木条做成一个等腰三角形(如图),这个等腰三角形各个内角的大小分别为多少(精确到1″)?
用三根长度分别为80cm,60cm,60cm的木条做成一个等腰三角形(如图),这个等腰三角形各个内角的大小分别为多少(精确到1″)?