题目内容
17.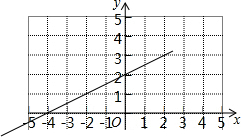 如图是某一次函数的图象,请根据图象回答问题;
如图是某一次函数的图象,请根据图象回答问题;(1)当x=0时,y=2;当y=0时,x=-4;
(2)写出相应的一次函数的表达式y=0.5x+2;
(3)一元一次方程$\frac{1}{2}$x+2=0的解和一次函数y=$\frac{1}{2}$x+2的图象有什么联系;
(4)一元一次方程$\frac{1}{2}$x+2>0的解集和一次函数y=$\frac{1}{2}$x+2的图象有什么联系.
分析 (1)根据图象得出直线与x,y轴的交点坐标解答即可;
(2)将交点坐标代入解析式,利用待定系数法得出解析式即可;
(3)根据一次函数与一元一次方程的关系解答即可;
(4)根据一元一次方程与一次函数的关系解答即可.
解答 解:(1)由图象可得:
直线与x轴的交点坐标为(-4,0),与y轴的交点坐标为(0,2),
所以可得:当x=0时,y=2;当y=0时,x=-4;
(2)设直线解析式为y=kx+b,
把(-4,0)(0,2)代入解析式可得:$\left\{\begin{array}{l}{b=2}\\{-4k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=0.5}\\{b=2}\end{array}\right.$.
所以解析式为:y=0.5x+2;
(3)方程$\frac{1}{2}x+2=0$的解是指函数$y=\frac{1}{2}x+2$在y=0时,函数图象与x轴的交点;
(4)$\frac{1}{2}$x+2>0的解集和一次函数y=$\frac{1}{2}$x+2的图象关系是:当x>-4时,y>0,
即:当x>-4时,在y=0.5x+2的图象上的所有点满足0.5x+2>0的要求.
故答案为:2;-4;y=0.5x+2.
点评 此题主要考查了一次函数与一元一次方程的关系,关键是根据图象得出解析式解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
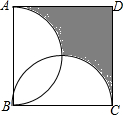 如图,正方形ABCD的边长为2,分别以AB、BC为直径,在正方形内作半圆,则图中阴影部分的面积为(3-$\frac{π}{2}$)平方单位.
如图,正方形ABCD的边长为2,分别以AB、BC为直径,在正方形内作半圆,则图中阴影部分的面积为(3-$\frac{π}{2}$)平方单位. 用三根长度分别为80cm,60cm,60cm的木条做成一个等腰三角形(如图),这个等腰三角形各个内角的大小分别为多少(精确到1″)?
用三根长度分别为80cm,60cm,60cm的木条做成一个等腰三角形(如图),这个等腰三角形各个内角的大小分别为多少(精确到1″)?