题目内容
9.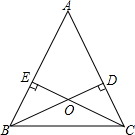 如图,锐角△ABC中AB=c,AC=b,BC=a且有b2-c2=ac-ab.
如图,锐角△ABC中AB=c,AC=b,BC=a且有b2-c2=ac-ab.(1)求证:△ABC是等腰三角形;
(2)作△ABC两条高BD、CE相交于点O,如果连接OA,试猜想直线OA与直线BC的位置关系并证明你的猜想.
分析 (1)由b2-c2=ac-ab,得到(b+c)(b-c)=-a(b-c),由于AB=c,AC=b,BC=a,于是得到当b-c=0时,等式才成立,即可得到结论;
(2)连接AO并延长交BC于M,根据等腰三角形的性质得到∠ABC=∠ACB,由垂直的定义得到∠BDC=∠CEB=90°,根据三角形的内角和得到∠OBC=∠OCB,根据等腰三角形的判定得到OB=OC,推出△ABO≌△ACO,根据等腰三角形的性质即可得到结论.
解答 证明:(1)∵b2-c2=ac-ab,
∴(b+c)(b-c)=-a(b-c),
∵AB=c,AC=b,BC=a,
∴当b-c=0时,等式才成立,
∴b=c,
∴△ABC是等腰三角形;
(2) 连接AO并延长交BC于M,
连接AO并延长交BC于M,
∵AB=AC,
∴∠ABC=∠ACB,
∵BD⊥AC,CE⊥AB,
∴∠BDC=∠CEB=90°,
∴∠OBC=∠OCB,
∴OB=OC,
在△ABO与△ACO中,
$\left\{\begin{array}{l}{AB=AC}\\{AO=AO}\\{BO=CO}\end{array}\right.$,
∴△ABO≌△ACO,
∴∠BAO=∠CAO,
∴AM⊥BC.
点评 本题考查了全等三角形的判定和性质,等腰三角形的判定和性质,熟练掌握全等三角形的判定和性质定理是解题的关键.

练习册系列答案
相关题目
19.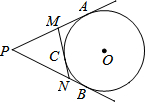 已知如图,PA、PB切⊙O于A、B,MN切⊙O于C,交PB于N;若PA=7.5cm,则△PMN的周长是( )
已知如图,PA、PB切⊙O于A、B,MN切⊙O于C,交PB于N;若PA=7.5cm,则△PMN的周长是( )
 已知如图,PA、PB切⊙O于A、B,MN切⊙O于C,交PB于N;若PA=7.5cm,则△PMN的周长是( )
已知如图,PA、PB切⊙O于A、B,MN切⊙O于C,交PB于N;若PA=7.5cm,则△PMN的周长是( )| A. | 7.5cm | B. | 10cm | C. | 15cm | D. | 12.5cm |
 用三根长度分别为80cm,60cm,60cm的木条做成一个等腰三角形(如图),这个等腰三角形各个内角的大小分别为多少(精确到1″)?
用三根长度分别为80cm,60cm,60cm的木条做成一个等腰三角形(如图),这个等腰三角形各个内角的大小分别为多少(精确到1″)?