题目内容
2.在直角梯形ABCD中,AD∥BC,∠B=90°,AB=BC=2AD,AD=2,若以CD为斜边作直角△CDE,且∠ECD的正切值为$\frac{1}{2}$,则AE=4.分析 根据平行线的性质得到∠A=90°,过D作DF⊥BC于F,推出四边形ABFD是矩形,求得BF=AD=2,CF=2,根据三角函数的定义得到tan∠FDC=$\frac{CF}{DF}$=$\frac{1}{2}$,由于∠ECD的正切值为$\frac{1}{2}$,得到∠FDC=∠ECD,证得A,D,E三点共线,由四边形ABCE是矩形,即可得到结论.
解答  解:如图1,∵AD∥BC,∠B=90°,
解:如图1,∵AD∥BC,∠B=90°,
∴∠A=90°,
∵AB=BC=2AD,AD=2,
∴AB=BC=4,
过D作DF⊥BC于F,
∴四边形ABFD是矩形,
∴BF=AD=2,
∴CF=2,
∴tan∠FDC=$\frac{CF}{DF}$=$\frac{1}{2}$,
∵∠ECD的正切值为$\frac{1}{2}$,
∴∠FDC=∠ECD,
∴∠EDC=∠CDF,
∴∠ADC+∠EDC=180°,
∴A,D,E三点共线,
∵∠E=90°,
∴四边形ABCE是矩形,
∴AE=BC=4.
如图2,∵∠A=∠B=∠DEC=90°,
∴四边形ABED是矩形,
∴BE=AD=2,DE=AB=4
∴CE=2,∴tan∠ECD=$\frac{DE}{CE}=2$,
∵∠ECD的正切值为$\frac{1}{2}$,
∴这种情况不存在,
综上所述:AE=4.
故答案为:4.
点评 本题考查了解直角三角形,矩形的判定和性质,梯形的性质,证明A,D,E三点共线是解题的关键.

练习册系列答案
相关题目
11.填空:
| 一元二次方程 | b2-4ac的值 | 方程根的情况 |
| x2-3x-6=0 | 33 | 两个不相等的实数根 |
| x2-4x=3 | 28 | 两个不相等的实数根 |
| x2+9=6x | 0 | 两个相等的实数根 |
| -2x2=3x+2 | -7 | 没有实数根 |
| x2-2$\sqrt{2}$ | 无 | 无 |
| 2x2-3=x2-2x | 16 | 两个不相等的实数根 |
 如图所示,在Rt△ABC中,BC=7.85,AB=11.40,解这个直角三角形.(边长保留三个有效数字,角度精确到1°)
如图所示,在Rt△ABC中,BC=7.85,AB=11.40,解这个直角三角形.(边长保留三个有效数字,角度精确到1°) 如图,点C、D、E在线段AB上,且AC=CD=DE=EB
如图,点C、D、E在线段AB上,且AC=CD=DE=EB 用三根长度分别为80cm,60cm,60cm的木条做成一个等腰三角形(如图),这个等腰三角形各个内角的大小分别为多少(精确到1″)?
用三根长度分别为80cm,60cm,60cm的木条做成一个等腰三角形(如图),这个等腰三角形各个内角的大小分别为多少(精确到1″)?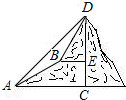 已知:如图,在山脚的A处测得山顶D的仰角为45°,沿着坡度为30°的斜角前进400米处到B处(即∠BAC=30°,AB=400米),测得D的仰角为60°,求山的高度CD.
已知:如图,在山脚的A处测得山顶D的仰角为45°,沿着坡度为30°的斜角前进400米处到B处(即∠BAC=30°,AB=400米),测得D的仰角为60°,求山的高度CD.