题目内容
16.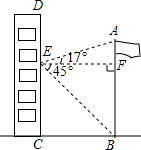 如图,在某次数学活动课中,小明为了测量校园内旗杆AB的高度,站在教学楼CD上的E处测得旗杆底端B的仰角∠BEF的度数为45°,测得旗杆顶端A的仰角∠AEF的度数为17°,旗杆底部B处与教学楼底部C处的水平距离BC为9m,求旗杆的高度(结果精确到0.1m).
如图,在某次数学活动课中,小明为了测量校园内旗杆AB的高度,站在教学楼CD上的E处测得旗杆底端B的仰角∠BEF的度数为45°,测得旗杆顶端A的仰角∠AEF的度数为17°,旗杆底部B处与教学楼底部C处的水平距离BC为9m,求旗杆的高度(结果精确到0.1m).【参考数据:sin17°=0.29,cos17°=0.96,tan17°=0.31】
分析 先根据锐角三角函数的定义求出BF及AF的长,再由AB=AF+BF即可得出结论.
解答 解:如图,由题意得EF=BC=9m,∠AEF=17°,∠BEF=45°,
在Rt△BEF中,
∵tan∠BEF=tan45°=$\frac{BF}{EF}$,
∴BF=EF=9m.
在Rt△AEF中,
∵tan17°=$\frac{AF}{EF}$,
∴AF=9×0.31=2.79m.
∴AB=AF+BF=11.79≈11.8m.
答:旗杆AB的高度约为11.8m.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,熟记锐角三角函数的定义是解答此题的关键.

练习册系列答案
相关题目
11.填空:
| 一元二次方程 | b2-4ac的值 | 方程根的情况 |
| x2-3x-6=0 | 33 | 两个不相等的实数根 |
| x2-4x=3 | 28 | 两个不相等的实数根 |
| x2+9=6x | 0 | 两个相等的实数根 |
| -2x2=3x+2 | -7 | 没有实数根 |
| x2-2$\sqrt{2}$ | 无 | 无 |
| 2x2-3=x2-2x | 16 | 两个不相等的实数根 |
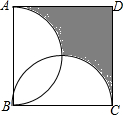 如图,正方形ABCD的边长为2,分别以AB、BC为直径,在正方形内作半圆,则图中阴影部分的面积为(3-$\frac{π}{2}$)平方单位.
如图,正方形ABCD的边长为2,分别以AB、BC为直径,在正方形内作半圆,则图中阴影部分的面积为(3-$\frac{π}{2}$)平方单位. 用三根长度分别为80cm,60cm,60cm的木条做成一个等腰三角形(如图),这个等腰三角形各个内角的大小分别为多少(精确到1″)?
用三根长度分别为80cm,60cm,60cm的木条做成一个等腰三角形(如图),这个等腰三角形各个内角的大小分别为多少(精确到1″)?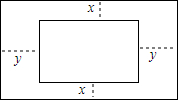 姥姥有一张长2米、宽1米的十字绣,她在十字绣的四周加上了花边做成了挂毯,上下花边宽度为x米,左右花边宽度为y米,若十字绣与挂毯是相似的长方形.
姥姥有一张长2米、宽1米的十字绣,她在十字绣的四周加上了花边做成了挂毯,上下花边宽度为x米,左右花边宽度为y米,若十字绣与挂毯是相似的长方形.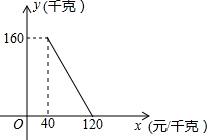 某商店以40元/千克的单价新近一批茶叶,经调查发现,在一段时间内,销量y(千克)与销售单价x(元/千克)之间的函数关系如图所示.
某商店以40元/千克的单价新近一批茶叶,经调查发现,在一段时间内,销量y(千克)与销售单价x(元/千克)之间的函数关系如图所示.