题目内容
2.计算$\frac{1}{4+\sqrt{59+30\sqrt{2}}}$+$\frac{1}{3-\sqrt{66-40\sqrt{2}}}$.分析 首先结合完全平方公式将根号下部分分解因式,进而分母有理化求出答案.
解答 解:原式=$\frac{1}{4+\sqrt{50+2\sqrt{450}+9}}$+$\frac{1}{3-\sqrt{50-2\sqrt{800}+16}}$
=$\frac{1}{4+\sqrt{(5\sqrt{2}+3)^{2}}}$+$\frac{1}{3-\sqrt{(5\sqrt{2}-4)^{2}}}$
=$\frac{1}{7+5\sqrt{2}}$+$\frac{1}{7-5\sqrt{2}}$
=5$\sqrt{2}$-7-7-5$\sqrt{2}$
=-14.
点评 此题主要考查了二次根式的化简求值,正确利用完全平方公式化简二次根式是解题关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
12. 如图,下面不能判断是平行四边形的是( )
如图,下面不能判断是平行四边形的是( )
 如图,下面不能判断是平行四边形的是( )
如图,下面不能判断是平行四边形的是( )| A. | ∠B=∠D,∠BAD=∠BCD | B. | AB∥CD,AD=BC | ||
| C. | ∠B+∠DAB=180°,∠B+∠BCD=180° | D. | AB∥CD,AB=CD |
11.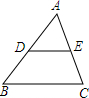 如图,已知D、E分别是△ABC的AB、AC边上的一点,DE∥BC,且AD:AB=1:2,则△ADE与四边形DBCE的面积之比为( )
如图,已知D、E分别是△ABC的AB、AC边上的一点,DE∥BC,且AD:AB=1:2,则△ADE与四边形DBCE的面积之比为( )
 如图,已知D、E分别是△ABC的AB、AC边上的一点,DE∥BC,且AD:AB=1:2,则△ADE与四边形DBCE的面积之比为( )
如图,已知D、E分别是△ABC的AB、AC边上的一点,DE∥BC,且AD:AB=1:2,则△ADE与四边形DBCE的面积之比为( )| A. | 1:4 | B. | 1:3 | C. | 1:2 | D. | 2:3 |
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给下以下结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给下以下结论: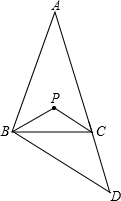 如图,在△ABC中,AB=AC,∠A=40°,延长AC到D,使CD=BC,点P是△ABD的内心,则∠BPC=145°.
如图,在△ABC中,AB=AC,∠A=40°,延长AC到D,使CD=BC,点P是△ABD的内心,则∠BPC=145°. 如图,由一副三角尺拼成的图形,写出∠C,∠EAD,∠CBE的度数.
如图,由一副三角尺拼成的图形,写出∠C,∠EAD,∠CBE的度数.