题目内容
12. 如图,下面不能判断是平行四边形的是( )
如图,下面不能判断是平行四边形的是( )| A. | ∠B=∠D,∠BAD=∠BCD | B. | AB∥CD,AD=BC | ||
| C. | ∠B+∠DAB=180°,∠B+∠BCD=180° | D. | AB∥CD,AB=CD |
分析 由平行四边形的判定方法得出选项A、C、D正确,选项B不正确,即可得出结论.
解答 解:∵∠B=∠D,∠BAD=∠BCD,
∴四边形ABCD是平行四边形,A选项正确;
∵AB∥CD,AD=BC,
∴四边形ABCD是等腰梯形,
不一定是平行四边形,B选项不正确;
∵∠B+∠DAB=180°,∠B+∠BCD=180°,
∴AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,C选项正确;
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,D选项正确.
故选B.
点评 本题考查了平行四边形的判定方法;熟记平行四边形的判定方法是解决问题的关键.

练习册系列答案
相关题目
12.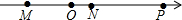 点M,N,P和原点O在数轴上的位置如图所示,点M,N,P对应的有理数为a,b,c(对应顺序暂不确定).如果ab<0,a+b>0,ac>bc,那么表示数b的点为( )
点M,N,P和原点O在数轴上的位置如图所示,点M,N,P对应的有理数为a,b,c(对应顺序暂不确定).如果ab<0,a+b>0,ac>bc,那么表示数b的点为( )
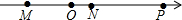 点M,N,P和原点O在数轴上的位置如图所示,点M,N,P对应的有理数为a,b,c(对应顺序暂不确定).如果ab<0,a+b>0,ac>bc,那么表示数b的点为( )
点M,N,P和原点O在数轴上的位置如图所示,点M,N,P对应的有理数为a,b,c(对应顺序暂不确定).如果ab<0,a+b>0,ac>bc,那么表示数b的点为( )| A. | 点M | B. | 点N | C. | 点P | D. | 点O |
3.已知点P1(1,3),点P2与点P1关于x轴对称,则P2的坐标是( )
| A. | (-5,-3) | B. | (1,-3) | C. | (-1,-3) | D. | (5,-3) |
1.用火柴棒按如图方式搭图形,按照这种方式搭下去,搭第8个图形需火柴棒的根数是( )


| A. | 48根 | B. | 50根 | C. | 52根 | D. | 54根 |
 如图,已知∠EAC是△ABC的外角,AD平分∠EAC,AB=AC.求证:AD∥BC.
如图,已知∠EAC是△ABC的外角,AD平分∠EAC,AB=AC.求证:AD∥BC.