题目内容
7.若a,b为实数,且a2+3a+1=0,b2+3b+1=0,求$\frac{b}{a}+\frac{a}{b}$的值.分析 当a和b相等时,原式=2;
当a和b不相等时,根据题意得到a、b是关于x的方程x2+3x+1=0的两个实数根,则利用根与系数的关系和完全平方公式的变形来求$\frac{b}{a}+\frac{a}{b}$的值.
解答 解:当a和b相等时,原式=2;
当a和b不相等时,依题意得:a、b是关于x的方程x2+3x+1=0的两个实数根,
则a+b=-3,ab=1,
所以$\frac{b}{a}+\frac{a}{b}$=$\frac{(a+b)^{2}-2ab}{ab}$=$\frac{(-3)^{2}-2×1}{1}$=7.
即$\frac{b}{a}+\frac{a}{b}$=7.
点评 本题考查了根与系数的关系.掌握根据题意得到a、b是关于x的方程x2+3x+1=0的两个实数根是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列说法中正确的是( )
| A. | -6既是负数、分数,也是有理数 | |
| B. | 0既不是正数、也不是负数,但是整数 | |
| C. | -200既是负数、也是整数,但不是有理数 | |
| D. | 以上都不正确 |
17.下列各式运算结果为正数的是( )
| A. | -3+7-5 | B. | (1-2)×3 | C. | -16÷(-3)2 | D. | -24×(-6) |
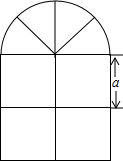 如图所示,一扇窗户的上部是由4个扇形组成的半圆形,下部是边长为a的4个小正方形组成,请计算这扇窗户的面积和窗框的总长.
如图所示,一扇窗户的上部是由4个扇形组成的半圆形,下部是边长为a的4个小正方形组成,请计算这扇窗户的面积和窗框的总长.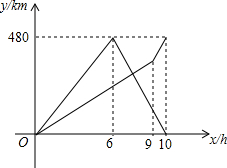 在一条笔直的公路,有A、B两地,甲从A地到B地,同时乙从B地到A地,途中两人相遇,乙到达A地后,立即按原路返回,遇到甲后两人一起回到B地.如图分别是两人各自离出发地的距离y(千米)与出发的时间x(小时)之间的函数图象,根据图象信息解答下列问题:
在一条笔直的公路,有A、B两地,甲从A地到B地,同时乙从B地到A地,途中两人相遇,乙到达A地后,立即按原路返回,遇到甲后两人一起回到B地.如图分别是两人各自离出发地的距离y(千米)与出发的时间x(小时)之间的函数图象,根据图象信息解答下列问题: