题目内容

11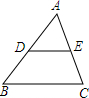．如图，已知D、E分别是△ABC的AB、AC边上的一点，DE∥BC，且AD：AB=1：2，则△ADE与四边形DBCE的面积之比为（　　）
A．1：4B．1：3C．1：2D．2：3

分析 因为DE∥BC，所以可得△ADE∽△ABC，根据相似三角形的面积比等于相似比的平方解答即可．

解答 解：∵DE∥BC，
∴△ADE∽△ABC，
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=（$\frac{AD}{AB}$）2=$\frac{1}{4}$，
∴$\frac{{S}_{△ADE}}{{S}_{四边形DBCE}}$=$\frac{1}{3}$．
故选B．

点评 本题考查了相似三角形的判定与性质，熟记相似三角形面积的比等于相似比的平方是解题的关键．

练习册系列答案
相关题目
1．用火柴棒按如图方式搭图形，按照这种方式搭下去，搭第8个图形需火柴棒的根数是（　　）
A．48根B．50根C．52根D．54根
2．计算$\frac{1}{4+\sqrt{59+30\sqrt{2}}}$+$\frac{1}{3-\sqrt{66-40\sqrt{2}}}$．
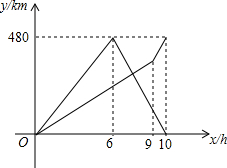19．在一条笔直的公路，有A、B两地，甲从A地到B地，同时乙从B地到A地，途中两人相遇，乙到达A地后，立即按原路返回，遇到甲后两人一起回到B地．如图分别是两人各自离出发地的距离y（千米）与出发的时间x（小时）之间的函数图象，根据图象信息解答下列问题：
（1）A、B两地的距离480千米，乙返回B时的速度120千米/小时．
（2）两人第一次相遇时，甲离出发地的距离．
（3）甲比按原速到达B地提前多少小时到家？
（4）请直接写出两人何时相距120千米．
6．解下列方程
（1）$\frac{2x-3}{x-1}=\frac{4x-1}{2x+3}$                                  
（2）$\frac{x}{x+2}+\frac{2}{2-x}$=1
（3）$\frac{x-1}{x+5}$=$\frac{x+5}{x-1}$                               
（4）$\frac{3}{x}+\frac{6}{x+1}=\frac{30}{x（x+1）}$．
16．若sin35°≈0.5712，则cos55°=0.5712．
3．4的绝对值的相反数的平方是（　　）
A．8B．16C．-16D．-8
20．有一点A（1，1），先向左平移2个单位得A1，再向下平移3个单位得A2，接着向右平移4个单位得A3，再向上平移5个单位得A4，紧接着向左平移6个单位得A5，再向下平移7个单位得A6，以此类推…，点A2015的坐标是（1009，-1008）．
1．某种品牌运动服经过两次降价，每件零售价由560元降为315元，已知两次降价的百分率相同，求每次降价的百分率．设每次降价的百分率为x，所列方程是560（1-x）2=315．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网