题目内容
15.如图,在△ABC中,∠CAB=90°,AB=AC,以AC为边作等边△ACD,连接BD.(1)求∠BDC的度数;
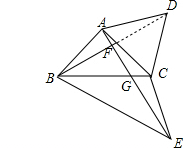
(2)如图2,将△BCD沿直线BC折叠得△BCE,点D关于直线BC对称点为E,连接AE,交BD于F,交BC于G,若FG=3,求GE的长.
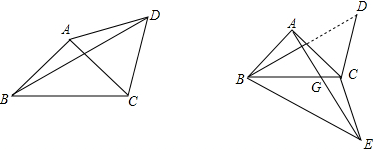
分析 (1)根据等腰直角三角形的性质得到∠ABC=∠ACB=45°,由△ACD是等边三角形,得到∠ACD=∠DAC=∠ADC=60°,于是得到∠BAD=150°,由于AB=AD,于是得到∠ADB=∠ABD=15°,即可得到结论;
(2)根据折叠的性质得到∠BEC=∠BDC=45°,∠BCE=∠BCD=45°+60°=105°,求出∠DBC=∠EBC=30°,证得∠BFG=90°,于是求得FG=$\frac{1}{2}$BG,然后根据等腰三角形的性质得到结论.
解答 解:(1)∵∠CAB=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵△ACD是等边三角形,
∴∠ACD=∠DAC=∠ADC=60°,
∴∠BAD=150°,
∵AB=AD,
∴∠ADB=∠ABD=15°,
∴∠BDC=45°;
(2) ∵将△BCD沿直线BC折叠得△BCE,
∵将△BCD沿直线BC折叠得△BCE,
∴∠BEC=∠BDC=45°,∠BCE=∠BCD=45°+60°=105°,
∴∠DBC=∠EBC=30°,
∵AC=CD=CE,∠ACE=∠ACB+∠BCE=150°,
∴∠CEG=15°,
∴∠GEB=30°,
∴∠FGB=60°
∴∠BFG=90°,
∴FG=$\frac{1}{2}$BG,
∵∠GBE=∠DBC=∠GEB=30°,
∴BG=GE,
∴GE=2FG=6.
点评 本题考查了翻折变换-折叠问题,等边三角形的性质,等腰直角三角形的性质,熟练掌握各性质定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.设a=-(-3-2)2,b=(-3)×(-2),c=(-3)2÷(-2)2,则( )
| A. | b>a>c | B. | b>c>a | C. | a>b>c | D. | c>a>b |
3.若a>b,则下列式子一定成立的是( )
| A. | a+3>b+5 | B. | 1-a>1-b | C. | a-9>b-9 | D. | ac2>bc2 |
10.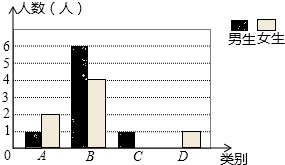 某校七年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如图表:
某校七年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如图表:
请你根据以上信息,解答下列问题:
(1)写出a,b,d的值并补全条形图;
(2)请你估计该校七年级共有多少名学生本次成绩不低于80分.
 某校七年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如图表:
某校七年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如图表:| 等级 | 分数 | 频数 | 频率 |
| A | 90≤x≤100 | 3 | 0.15 |
| B | 80≤x<90 | 10 | a |
| C | 70≤x<80 | b | 0.2 |
| D | 60≤x<70 | c | d |
| 合计 | 1 |
(1)写出a,b,d的值并补全条形图;
(2)请你估计该校七年级共有多少名学生本次成绩不低于80分.
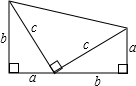 利用如图来证明勾股定理.
利用如图来证明勾股定理.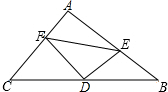 如图所示,在△ABC中,∠A=90°,D为BC的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,试探究线段BE,EF,FC之间的数量关系.
如图所示,在△ABC中,∠A=90°,D为BC的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,试探究线段BE,EF,FC之间的数量关系.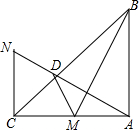 如图,AB⊥AC,NC⊥AC,AB=AC,M为AC中点,AN⊥BM交BC于D,BC平分∠ACN.求证:
如图,AB⊥AC,NC⊥AC,AB=AC,M为AC中点,AN⊥BM交BC于D,BC平分∠ACN.求证: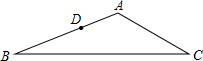 如图,在△ABC中,AB=12cm,BC=18cm,AC=9cm,D为AB上一点,BD=$\frac{2}{3}$AB,E是AC上的一点.若△ADE与△ABC相似,请你画出线段DE并求DE的长.
如图,在△ABC中,AB=12cm,BC=18cm,AC=9cm,D为AB上一点,BD=$\frac{2}{3}$AB,E是AC上的一点.若△ADE与△ABC相似,请你画出线段DE并求DE的长.