题目内容
6.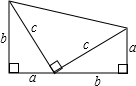 利用如图来证明勾股定理.
利用如图来证明勾股定理.
分析 用面积分割法法证明勾股定理:梯形的面积=3个三角形面积的和,依此即可证明.
解答 证明:梯形的面积为$\frac{1}{2}$(a+b)(a+b)=$\frac{1}{2}$(a+b)2;
另一方面,梯形可分成三个直角三角形,其面积又可以表示成$\frac{1}{2}$ab+$\frac{1}{2}$ab+$\frac{1}{2}$c2.
所以$\frac{1}{2}$(a+b)2=$\frac{1}{2}$ab+$\frac{1}{2}$ab+$\frac{1}{2}$c2.
即a2+b2=c2.
点评 本题考查了勾股定理的证明,利用梯形的面积和三角形的面积计算方法建立等式是解决问题的关键.

练习册系列答案
相关题目
 如图,已知在△ABC中,∠C=90°,AB的垂直平分线交BC于D,垂足为E,∠CAD:∠DAB=2:1,求∠BAC的度数.
如图,已知在△ABC中,∠C=90°,AB的垂直平分线交BC于D,垂足为E,∠CAD:∠DAB=2:1,求∠BAC的度数.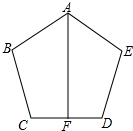 已知BC=ED,AB=AE,∠B=∠E,F是CD的中点,求证:AF⊥CD.
已知BC=ED,AB=AE,∠B=∠E,F是CD的中点,求证:AF⊥CD. 如图,O2是⊙O1上的一点,以O2为圆心,O1O2为半径作⊙O2,与⊙O1交于点A、B,那么∠AO1B的度数为120°.
如图,O2是⊙O1上的一点,以O2为圆心,O1O2为半径作⊙O2,与⊙O1交于点A、B,那么∠AO1B的度数为120°.