题目内容
5.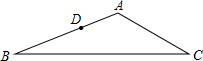 如图,在△ABC中,AB=12cm,BC=18cm,AC=9cm,D为AB上一点,BD=$\frac{2}{3}$AB,E是AC上的一点.若△ADE与△ABC相似,请你画出线段DE并求DE的长.
如图,在△ABC中,AB=12cm,BC=18cm,AC=9cm,D为AB上一点,BD=$\frac{2}{3}$AB,E是AC上的一点.若△ADE与△ABC相似,请你画出线段DE并求DE的长.
分析 分△ADE∽△ABC和△ADE∽△ACB两种情况,根据相似三角形的性质进行计算即可.
解答 解: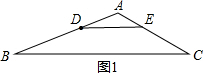 如图1,△ADE∽△ABC,
如图1,△ADE∽△ABC,
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$,
又∵BD=$\frac{2}{3}$AB,AB=12cm,BC=18cm,
∴DE=6cm;
如图2,△ADE∽△ACB,
∴$\frac{AD}{AC}$=$\frac{DE}{BC}$,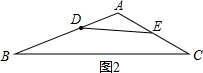
∵BD=$\frac{2}{3}$AB,AB=12cm,
∴AD=4cm,
又∵BC=18cm,
∴DE=8cm.
答:DE的长是6cm或8cm.
点评 本题考查的是相似三角形的性质,掌握相似三角形的对应角相等,对应边的比相等是解题的关键,注意分情况讨论思想的应用.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
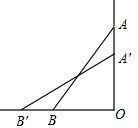 如图,一架长2.5m的梯子,斜放在墙上,梯子的底部B离墙角O的距离是0.7m,当梯子的顶部A向下滑0.4m到A′时,梯子的底部向外移动0.8m.
如图,一架长2.5m的梯子,斜放在墙上,梯子的底部B离墙角O的距离是0.7m,当梯子的顶部A向下滑0.4m到A′时,梯子的底部向外移动0.8m.