Question

4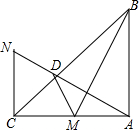．如图，AB⊥AC，NC⊥AC，AB=AC，M为AC中点，AN⊥BM交BC于D，BC平分∠ACN．求证：
（1）△ABM≌△CAN；
（2）∠AMB=∠CMD．

Answer 1

分析 （1）利用已知条件用ASA证明△ABM≌△CAN；
（2）由△ABM≌△CAN，得到AM=CN，∠AMB=∠N，再证明△MCD≌△NCD（SAS），得到∠CMD=∠N，即可解答．

解答 解：（1）∵AB⊥AC，NC⊥AB，
∴∠BAM=∠ACN=90°，
∵∠MBA+∠BMA=90°，
∠NAC+∠BMA=90°（AN⊥BM），
∴∠MBA=∠NAC，
在△ABM和△CAN中，
$\left\{\begin{array}{l}{∠ACN=∠BAM=9{0}^{°}}\\{AC=BC}\\{∠NAC=∠MBA}\end{array}\right.$
∴△ABM≌△CAN（ASA）
（2）∵△ABM≌△CAN，
∴AM=CN，∠AMB=∠N，
∵M为AC中点，
∴AM=CM
∴CM=CN
∵BC平分∠ACN
∴∠MCD=∠NCD
在△MCD和△NCD中，
$\left\{\begin{array}{l}{CM=CN}\\{∠MCD=∠NCD}\\{CD=CD}\end{array}\right.$
∴△MCD≌△NCD（SAS）
∴∠CMD=∠N，
∴∠AMB=∠CMD．

点评 本题考查了全等三角形的性质与判定，解决本题的关键是证明△ABM≌△CAN，△MCD≌△NCD．