题目内容
6.一列数a1,a2,a3,…满足条件:a1=$\frac{1}{2}$,an=$\frac{1}{1{-a}_{n-1}}$(n≥2,且n为整数),则a2017等于( )| A. | -1 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
分析 求出数列的前4项,继而得出数列的循环周期,然后根据所得的规律进行求解即可.
解答 解:∵a1=$\frac{1}{2}$,an=$\frac{1}{1{-a}_{n-1}}$,
∴a2=$\frac{1}{1-{a}_{1}}$=$\frac{1}{1-\frac{1}{2}}$=2,
a3=$\frac{1}{1-{a}_{2}}$=$\frac{1}{1-2}$=-1,
a4=$\frac{1}{1-{a}_{3}}$=$\frac{1}{1-(-1)}$=$\frac{1}{2}$,
…
∴这列数每3个数为一循环周期,
∵2017÷3=672…1,
∴a2017=a1=$\frac{1}{2}$,
故选B.
点评 此题主要考查了数字变化规律问题,认真观察、仔细思考,善用联想是解决这类问题的方法,解题时注意运用an=$\frac{1}{1{-a}_{n-1}}$进行计算.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
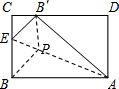 将矩形纸片ABCD折叠,使点B落在边CD上的B'处,折痕为AE,已知AB=5,AD=4.
将矩形纸片ABCD折叠,使点B落在边CD上的B'处,折痕为AE,已知AB=5,AD=4.
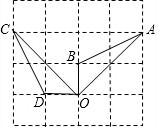 如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针旋转到△COD的位置,则旋转角为90°.
如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针旋转到△COD的位置,则旋转角为90°.