题目内容
18.在-3、-2、-1、0、1、2这六个数中,随机取出一个数,记为m,若数m使关于x的分式方程$\frac{1}{2x-1}$-1=$\frac{m}{1-2x}$的解是正实数或零,且使得的二次函数y=-x2+(2m-1)x+1的图象,在x>1时,y随x的增大而减小,则满足条件的所有m之和是( )| A. | -2 | B. | -1 | C. | 0 | D. | 2 |
分析 通过解分式方程找出分式方程的解为x=1+$\frac{m}{2}$且x≠$\frac{1}{2}$,由其为正实数或零即可得出m的值,再根据二次函数的性质可找出关于m的一元一次不等式,解之即可得出m的取值范围,从而可确定m的值,将其相加即可得出结论.
解答 解:分式方程$\frac{1}{2x-1}$-1=$\frac{m}{1-2x}$的解为x=1+$\frac{m}{2}$且x≠$\frac{1}{2}$,
∵x=1+$\frac{m}{2}$为正实数或零且x≠$\frac{1}{2}$,
∴m=-2、0、1、2.
∵二次函数y=-x2+(2m-1)x+1的图象,在x>1时,y随x的增大而减小,
∴$\frac{2m-1}{2}$≤1,
解得:m≤$\frac{3}{2}$,
∴m=-2、0、1,
∴-2+0+1=-1.
故选B.
点评 本题考查了二次函数的性质、分式方程的解以及解一元一次不等式,通过解分式方程以及二次函数的性质,找出m的值是解题的关键.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
6.一列数a1,a2,a3,…满足条件:a1=$\frac{1}{2}$,an=$\frac{1}{1{-a}_{n-1}}$(n≥2,且n为整数),则a2017等于( )
| A. | -1 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
6.若不等式a(x-1)-5(2x-3)≥4-3x的解集为x≤2,则a的值为( )
| A. | 1 | B. | 2 | C. | -2 | D. | 3 |
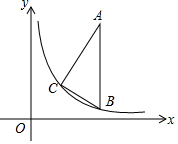 如图,在直角△ABC中,∠C=90°,∠A=30°,AB∥y轴,且AB=6,顶点B,C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,且点B的横坐标为2$\sqrt{3}$,则k=$\sqrt{3}$.
如图,在直角△ABC中,∠C=90°,∠A=30°,AB∥y轴,且AB=6,顶点B,C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,且点B的横坐标为2$\sqrt{3}$,则k=$\sqrt{3}$.