题目内容
17.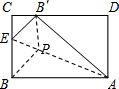 将矩形纸片ABCD折叠,使点B落在边CD上的B'处,折痕为AE,已知AB=5,AD=4.
将矩形纸片ABCD折叠,使点B落在边CD上的B'处,折痕为AE,已知AB=5,AD=4.(1)求B'C的长;
(2)过点B'作B'P∥BC,交AE于点P,求B'P的长.
分析 (1)由矩形的性质得到AD=BC=4,CD=AB=5,∠C=∠D=90°,由折叠的性质得,AB=AB′=5,B′E=BE,根据勾股定理即可得到结论;
(2)根据平行线的性质得到∠BEP=∠B′PE,由折叠的性质得到∠BEP=∠B′EP,等量代换得到∠B′EP=∠B′PE,根据等腰三角形的性质得到B′P=B′E=BE,根据勾股定理即可得到结论.
解答 解:(1)∵四边形ABCD是矩形,
∴AD=BC=4,CD=AB=5,∠C=∠D=90°,
由折叠的性质得,AB=AB′=5,B′E=BE,
∴DB′=$\sqrt{AB{′}^{2}-A{D}^{2}}$=3,
∴B′C=CD-DB′=2;
(2)∵B'P∥BC,
∴∠BEP=∠B′PE,
由折叠的性质得,∠BEP=∠B′EP,
∴∠B′EP=∠B′PE,
∴B′P=B′E=BE,
∵B′C2+CE2=B′E2,
∴22+(4-B′P)2=B′P2,
∴B′P=$\frac{5}{2}$.
点评 本题考查了翻折变换(折叠问题),矩形的性质,解直角三角形,平行线的性质,正确的识别图形是解题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
7. 如图,在平面直角坐标系中,函数y=$\frac{k}{x}$(x<0)的图象经过点P,则k的值为( )
如图,在平面直角坐标系中,函数y=$\frac{k}{x}$(x<0)的图象经过点P,则k的值为( )
 如图,在平面直角坐标系中,函数y=$\frac{k}{x}$(x<0)的图象经过点P,则k的值为( )
如图,在平面直角坐标系中,函数y=$\frac{k}{x}$(x<0)的图象经过点P,则k的值为( )| A. | -5 | B. | -6 | C. | 5 | D. | 6 |
12.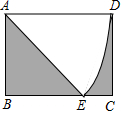 在矩形ABCD中,AB=$\sqrt{2}$,BC=2,以A为圆心,AD为半径画弧交线段BC于E,连接DE,则阴影部分的面积为( )
在矩形ABCD中,AB=$\sqrt{2}$,BC=2,以A为圆心,AD为半径画弧交线段BC于E,连接DE,则阴影部分的面积为( )
 在矩形ABCD中,AB=$\sqrt{2}$,BC=2,以A为圆心,AD为半径画弧交线段BC于E,连接DE,则阴影部分的面积为( )
在矩形ABCD中,AB=$\sqrt{2}$,BC=2,以A为圆心,AD为半径画弧交线段BC于E,连接DE,则阴影部分的面积为( )| A. | $\frac{π}{4}$ | B. | 2$\sqrt{2}$-$\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | 2$\sqrt{2}$-$\frac{π}{2}$ |
6.一列数a1,a2,a3,…满足条件:a1=$\frac{1}{2}$,an=$\frac{1}{1{-a}_{n-1}}$(n≥2,且n为整数),则a2017等于( )
| A. | -1 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |