题目内容
8.九年级学生去测量校园人工湖的深度,他们把一根竹竿插到离湖边2m的水底,只见竹竿高出水面1m,把竹竿的顶端拉向湖边(底端没动),竿顶和湖沿的水面刚好平齐,则湖水的深度为1.5m.分析 设湖水深hm,则竹竿高(h+1)m,再根据勾股定理求出h的值即可.
解答  解:如图所示:设湖水深hm,则竹竿高(h+1)m,
解:如图所示:设湖水深hm,则竹竿高(h+1)m,
在Rt△BOC中,
∵OB=h,BC=h+1,OC=2m,
∴22+h2=(h+1)2,
解得:h=1.5,
故答案为:1.5m.
点评 本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
相关题目
11.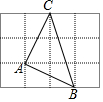 如图,将△ABC放在正方形网格中(图中每个小正方形边长均为1)点A,B,C恰好在网格图中的格点上,那么∠ABC的度数为( )
如图,将△ABC放在正方形网格中(图中每个小正方形边长均为1)点A,B,C恰好在网格图中的格点上,那么∠ABC的度数为( )
 如图,将△ABC放在正方形网格中(图中每个小正方形边长均为1)点A,B,C恰好在网格图中的格点上,那么∠ABC的度数为( )
如图,将△ABC放在正方形网格中(图中每个小正方形边长均为1)点A,B,C恰好在网格图中的格点上,那么∠ABC的度数为( )| A. | 90° | B. | 60° | C. | 30° | D. | 45° |
20.下列命题中,真命题是( )
| A. | 在同一平面内,过一点可作一条直线与已知直线垂直 | |
| B. | 过一点可作一条直线与已知直线平行 | |
| C. | 三条直线两两相交有三个交点 | |
| D. | 垂直于同一条直线的两条直线平行 |
17.计算5-(-2)×3的结果等于( )
| A. | -11 | B. | -1 | C. | 1 | D. | 11 |
 一次函数y=kx+b的图象如图所示,则不等式kx+b>0的解集是x<3.
一次函数y=kx+b的图象如图所示,则不等式kx+b>0的解集是x<3. 如图是某建筑物的屋顶架,其中AB=8m,D是AB的中点,BC,DE都垂直于AC.如果∠ABC=60°,那么BC,DE,CD各是多少米?
如图是某建筑物的屋顶架,其中AB=8m,D是AB的中点,BC,DE都垂直于AC.如果∠ABC=60°,那么BC,DE,CD各是多少米?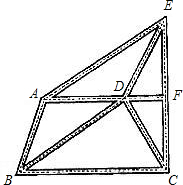 已知:如图是某城市部分街道示意图,AF∥BC,且AF⊥CE,AB=DC,AB∥DE,BD∥AE.甲、乙两人同时从B站乘车到F站,甲乘1路车,路线是B→A→E→F,乙乘2路车,路线是B→D→C→F,假设两车速度相同,途中耽误时间相同,那么谁先到达F站?说明理由.
已知:如图是某城市部分街道示意图,AF∥BC,且AF⊥CE,AB=DC,AB∥DE,BD∥AE.甲、乙两人同时从B站乘车到F站,甲乘1路车,路线是B→A→E→F,乙乘2路车,路线是B→D→C→F,假设两车速度相同,途中耽误时间相同,那么谁先到达F站?说明理由.