题目内容
3. 如图是某建筑物的屋顶架,其中AB=8m,D是AB的中点,BC,DE都垂直于AC.如果∠ABC=60°,那么BC,DE,CD各是多少米?
如图是某建筑物的屋顶架,其中AB=8m,D是AB的中点,BC,DE都垂直于AC.如果∠ABC=60°,那么BC,DE,CD各是多少米?
分析 根据直角三角形两锐角互余列式计算即可得到∠A,再根据直角三角形30°角所对的直角边等于斜边的一半可得BC=$\frac{1}{2}$AB,然后判断出DE是△ABC的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半解答,再根据CD=$\frac{1}{2}$CD即可解决问题.
解答 解:∵∠ABC=60°,立柱BC垂直于横梁AC,
∴∠A=90°-60°=30°;
∴BC=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4(cm),
∵点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,
∴DE是△ABC的中位线,
∴DE=$\frac{1}{2}$BC=$\frac{1}{2}$×4=2(cm).
∵CD=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4(cm).
点评 本题考查勾股定理的应用、解直角三角形、锐角三角函数、等腰三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
9.在△ABC中,若a=$\sqrt{2n}$,b=$\sqrt{{n}^{2}+1}$,c=n-1,则△ABC的形状是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 等腰三角形 | D. | 直角三角形 |
12.已知实数a满足|2016-a|+$\sqrt{a-2017}$=a,那么a-20162的值是( )
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |
 如图,已知CD平分∠ACB,∠1=∠2,试判断AC与DE的位置关系,并说明理由.
如图,已知CD平分∠ACB,∠1=∠2,试判断AC与DE的位置关系,并说明理由.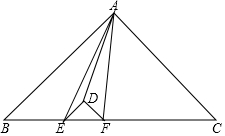 如图,等腰直角三角形DEF的斜边在等腰直角三角形ABC的斜边上,连接AE、AD、AF,于是整个图形被分成五块小三角形.其中三块的面积为S△DEF=1、S△ADE=2、S△ADF=3,那么△ABC的面积是36.
如图,等腰直角三角形DEF的斜边在等腰直角三角形ABC的斜边上,连接AE、AD、AF,于是整个图形被分成五块小三角形.其中三块的面积为S△DEF=1、S△ADE=2、S△ADF=3,那么△ABC的面积是36.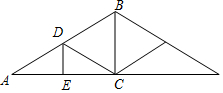 如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DE都垂直于横梁AC,其中AB=8.4m,∠A=30°,则立柱BC与DE的和为6.3 m.
如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DE都垂直于横梁AC,其中AB=8.4m,∠A=30°,则立柱BC与DE的和为6.3 m.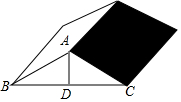 如图所示是某工厂长方屋顶的人字架(等腰三角形),它的跨度BC=12米,中柱AD为2.5米,中柱AD⊥BC,且垂足D为BC的中点,又知厂房长20米,为防雨,需在房顶铺满油毡.(每卷油毡宽1米,长10米),如果你是该厂采购,需购买多少卷油毡?
如图所示是某工厂长方屋顶的人字架(等腰三角形),它的跨度BC=12米,中柱AD为2.5米,中柱AD⊥BC,且垂足D为BC的中点,又知厂房长20米,为防雨,需在房顶铺满油毡.(每卷油毡宽1米,长10米),如果你是该厂采购,需购买多少卷油毡?