题目内容
13.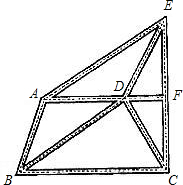 已知:如图是某城市部分街道示意图,AF∥BC,且AF⊥CE,AB=DC,AB∥DE,BD∥AE.甲、乙两人同时从B站乘车到F站,甲乘1路车,路线是B→A→E→F,乙乘2路车,路线是B→D→C→F,假设两车速度相同,途中耽误时间相同,那么谁先到达F站?说明理由.
已知:如图是某城市部分街道示意图,AF∥BC,且AF⊥CE,AB=DC,AB∥DE,BD∥AE.甲、乙两人同时从B站乘车到F站,甲乘1路车,路线是B→A→E→F,乙乘2路车,路线是B→D→C→F,假设两车速度相同,途中耽误时间相同,那么谁先到达F站?说明理由.
分析 连接AC,可知四边形ABCD为等腰梯形,四边形ABDE为平行四边形,则可比较两路线的长短,可求得答案.
解答  解:同时到达,理由如下:
解:同时到达,理由如下:
连接AC,如图,
∵AF∥BC,AB=CD,
∴四边形ABCD为等腰梯形,
∴AC=BD,
∵AB∥DE,BD∥AE,
∴四边形ABDE为平行四边形,
∴AE=BD=AC,AB=DE,
∵AF⊥CE,
∴AF为线段CE的垂直平分线,
∴CF=EF,
∴甲乘1路车,路程=BA+AE+EF=CD+BD+CF,
乙乘2路车,路程=BD+DC+CF,
∴两人同时到达.
点评 本题主要考查平行四边形的性质,掌握平行四边形的对边相等是解题的关键.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
18.已知反比例函数y=$\frac{m-3}{x}$的图象经过第一、三象限,则符合条件的m是( )
| A. | m=-1 | B. | m=0 | C. | m=3 | D. | m=5 |
18. 如图,AB∥CD,若∠1=40°,∠2=65°,则∠CAD=( )
如图,AB∥CD,若∠1=40°,∠2=65°,则∠CAD=( )
 如图,AB∥CD,若∠1=40°,∠2=65°,则∠CAD=( )
如图,AB∥CD,若∠1=40°,∠2=65°,则∠CAD=( )| A. | 50° | B. | 65° | C. | 75° | D. | 85° |
2.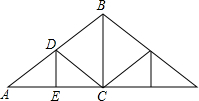 如图,屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=8m,∠A=30°,则BC和DE的长分别等于( )
如图,屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=8m,∠A=30°,则BC和DE的长分别等于( )
 如图,屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=8m,∠A=30°,则BC和DE的长分别等于( )
如图,屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=8m,∠A=30°,则BC和DE的长分别等于( )| A. | 2m,2m | B. | 4m,2m | C. | 2m,4m | D. | 4m,4m |
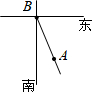 如图,如果张江高科技园区(A)位于复旦大学(B)的南偏东30°的方向,那么复旦大学(B)位于张江高科技园区(A)的北偏西30°或西偏北60°方向.
如图,如果张江高科技园区(A)位于复旦大学(B)的南偏东30°的方向,那么复旦大学(B)位于张江高科技园区(A)的北偏西30°或西偏北60°方向.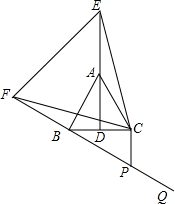 如图,在等边△ABC中,已知AD是∠BAC的角平分线,E为AD延长线上一点,以CE为一边且在CE以左作等边△CEF,连接BF.
如图,在等边△ABC中,已知AD是∠BAC的角平分线,E为AD延长线上一点,以CE为一边且在CE以左作等边△CEF,连接BF.