题目内容
20.计算(x+a)(x+b)得x2+(a+b)x+ab,若(x+a)(x+b)=x2+mx+3,则整数m的所有可能的值是±4.分析 根据题意可知:ab=3,a+b=m,从而可求出m的值.
解答 解:由(x+a)(x+b)得x2+(a+b)x+ab,
∴(x+a)(x+b)=x2+mx+3,可知ab=3,a+b=m,
∵m是整数,
∴a、b都是整数,
∴a、b有以下情况,
a=1,b=3,
a=-1,b=-3
a=3,b=1
a=-3,b=-1
∴m=a+b=±4,
故答案为:±4
点评 本题考查多项式乘以多项式,解题的关键是由题意得出ab=3,a+b=m,本题属于基础题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.某物流公司规定:办理托运业务,当物品的重量不超过16千克时,需付基础费30元和保险费a元;当物品重量超过16千克时,除了付以上的基础费和保险费外,超过部分还需付每千克b元的超重费.右表是该公司最近承接托运的两包物品重量和所收取的费用.
试问在物品可拆分的情况下,托运55千克物品的最少费用是( )
| 物品重量(千克) | 收取费用(元) |
| 18 | 39 |
| 25 | 60 |
| A. | 120 | B. | 132 | C. | 135 | D. | 150 |
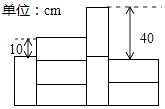 如图所示是由截面为同一种矩形的墙砖粘贴的部分墙面,其中三块横放的墙砖比一块竖放的墙砖高10cm,两块横放的墙砖比两块竖放的墙砖低40cm,则每块墙砖的截面面积是525cm2.
如图所示是由截面为同一种矩形的墙砖粘贴的部分墙面,其中三块横放的墙砖比一块竖放的墙砖高10cm,两块横放的墙砖比两块竖放的墙砖低40cm,则每块墙砖的截面面积是525cm2.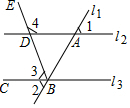 如图所示,直线l1与l2,l3相交于A,B两点,∠ABC的平分线交l2于点D,已知∠1=∠2=62°.
如图所示,直线l1与l2,l3相交于A,B两点,∠ABC的平分线交l2于点D,已知∠1=∠2=62°.