题目内容
15.某物流公司规定:办理托运业务,当物品的重量不超过16千克时,需付基础费30元和保险费a元;当物品重量超过16千克时,除了付以上的基础费和保险费外,超过部分还需付每千克b元的超重费.右表是该公司最近承接托运的两包物品重量和所收取的费用.| 物品重量(千克) | 收取费用(元) |
| 18 | 39 |
| 25 | 60 |
| A. | 120 | B. | 132 | C. | 135 | D. | 150 |
分析 根据题意可以列出相应的方程组,求出a、b的值,由题意可知33元可以托运16千克,如果超出部分只要不差过33÷3=11(千克),就可以直接托运,超出11千克就选择再另外运送,从而可以求得最低费用.
解答 解:由题意可得,
$\left\{\begin{array}{l}{30+a+(18-16)b=39}\\{30+a+(25-16)b=60}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{a=3}\\{b=3}\end{array}\right.$,
∴当物品的重量不超过16千克时,需付费33元,超过部分还需付每千克3元的超重费,
∴在物品可拆分的情况下,托运55千克物品的最少费用是:33+33+[33+(55-16-16-16)×3]=120(元),
故选A.
点评 本题考查二元一次方程组的应用,解答本题的关键是明确题意,列出相应的方程组,利用方程的思想解答.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
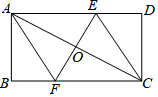 如图,四边形ABCD为矩形,O为AC中点,过点O作AC的垂线分别交AD、BC于点E、F,连接AF、CE.
如图,四边形ABCD为矩形,O为AC中点,过点O作AC的垂线分别交AD、BC于点E、F,连接AF、CE.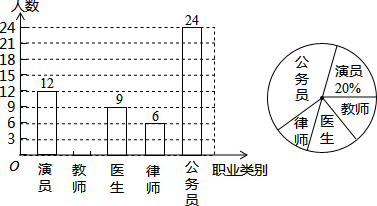
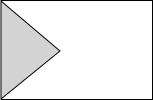 如图,在周长为12cm的矩形铁板上剪去一个等腰直角三角形(这个等腰直角三角形的底是矩形的宽),则矩形的宽为$\frac{12}{5}$cm时,剩下铁板的面积最大.
如图,在周长为12cm的矩形铁板上剪去一个等腰直角三角形(这个等腰直角三角形的底是矩形的宽),则矩形的宽为$\frac{12}{5}$cm时,剩下铁板的面积最大.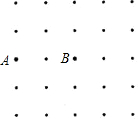 如图,由25个点构成一个正方形点阵,横纵方向相邻的两点之间的距离都是1个单位,以A,B为顶点,再选择两个点构成一个面积为2的平行四边形,这样的平行四边形共有9个.
如图,由25个点构成一个正方形点阵,横纵方向相邻的两点之间的距离都是1个单位,以A,B为顶点,再选择两个点构成一个面积为2的平行四边形,这样的平行四边形共有9个.