题目内容
8.为发展校园足球运动,巫溪县某五所初中决定联合购买一批耐克足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球.已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球:乙商场优惠方案是:若购买队服超过90套,则购买足球打八折.(1)求每套队服和每个足球的价格是多少?
(2)若五校联合购买100套队服和m个足球(其中m>30),请用含m的式子分别表示出到甲商场和乙商场购买装备所花的费用,假如你是本次购买任务的负责人,要采购100套队服和60个足球,你认为到哪家商场购买比较合算?
分析 (1)设每个足球的价格为x元,则每套队服的价格为(x+50)元,根据两套队服与三个足球的费用相等,即可得出关于x的一元一次方程,解之即可得出结论;
(2)根据两商城的优惠方案找出总费用w甲、w乙关于足球个数m的函数关系式,代入m=60求出两值,比较后即可得出结论.
解答 解:(1)设每个足球的价格为x元,则每套队服的价格为(x+50)元,
根据题意得:2(x+50)=3x,
解得:x=100,
∴x+50=150.
答:每个足球的价格为100元,每套队服的价格为150元.
(2)甲商城所需费用w甲=100×150+100(m-10)=100m+14000,
乙商场所需费用w乙=100×150+100×0.8m=80m+15000.
当m=60时,w甲=100m+14000=20000,w乙=80m+15000=19800,
∵20000>19800,
∴要采购100套队服和60个足球,到乙商场购买比较合算.
点评 本题考查了一元一次方程的应用以及一次函数图象上点的坐标特征,解题的关键是:(1)根据两套队服与三个足球的费用相等,列出关于x的一元一次方程;(2)根据数量关系,找出w甲、w乙关于m的函数关系式.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
17.受寒潮影响,淘宝网上的电热取暖器销售火旺,某电商销售每台成本价分别为200元、170元的A、B两种型号的电热取暖器,下表是近两天的销售情况:
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电热取暖器的销售单价;
(2)若电商准备用不多于5400元的金额再采购这两种型号的电热取暖器共30台,求A种型号的电热取暖器最多能采购多少台?
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一天 | 3台 | 5台 | 1800元 |
| 第二天 | 4台 | 10台 | 3100元 |
(1)求A、B两种型号的电热取暖器的销售单价;
(2)若电商准备用不多于5400元的金额再采购这两种型号的电热取暖器共30台,求A种型号的电热取暖器最多能采购多少台?
 已知:如图,点C是线段AB的中点,CE=CD,∠ACD=∠BCE,求证:AE=BD.
已知:如图,点C是线段AB的中点,CE=CD,∠ACD=∠BCE,求证:AE=BD.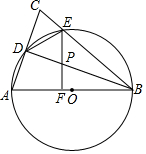 已知:如图,在△ABC中,AB=BC=10,以AB为直径作⊙O分别交AC,BC于点D,E,连接DE和DB,过点E作EF⊥AB,垂足为F,交BD于点P.
已知:如图,在△ABC中,AB=BC=10,以AB为直径作⊙O分别交AC,BC于点D,E,连接DE和DB,过点E作EF⊥AB,垂足为F,交BD于点P.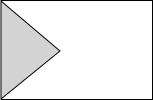 如图,在周长为12cm的矩形铁板上剪去一个等腰直角三角形(这个等腰直角三角形的底是矩形的宽),则矩形的宽为$\frac{12}{5}$cm时,剩下铁板的面积最大.
如图,在周长为12cm的矩形铁板上剪去一个等腰直角三角形(这个等腰直角三角形的底是矩形的宽),则矩形的宽为$\frac{12}{5}$cm时,剩下铁板的面积最大. 小红家用10m长的铁丝在墙边围成了一个长方形鸡棚,若鸡棚的长AB比宽BC多5m,且宽的一边有一扇1m宽的门,求该鸡棚的面积.
小红家用10m长的铁丝在墙边围成了一个长方形鸡棚,若鸡棚的长AB比宽BC多5m,且宽的一边有一扇1m宽的门,求该鸡棚的面积.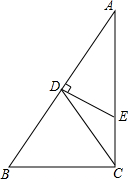 在Rt△ABC中,∠ACB=90°,D为AB边上的中点,DE⊥AB,AD=2DE.
在Rt△ABC中,∠ACB=90°,D为AB边上的中点,DE⊥AB,AD=2DE.