题目内容
某商场现在的售价为每件80元,每星期可卖出200件,市场调查反应:销售单价每降低1元,每星期就可多售出20件,已知商品的进价为每件60元
(1)写出每星期的销售量y(件)与销售单价x(x<80)(元)之间的函数关系式;
(2)若销售该该商品每月获得利润为W元,写出利润w与销售单价x之间的函数关系式;
(3)若某商场规定该商品销售单价不低于76元,且商场要完成每星期不少于240件的销售任务,则商场销售该商品获得的最大利润是多少?
(1)写出每星期的销售量y(件)与销售单价x(x<80)(元)之间的函数关系式;
(2)若销售该该商品每月获得利润为W元,写出利润w与销售单价x之间的函数关系式;
(3)若某商场规定该商品销售单价不低于76元,且商场要完成每星期不少于240件的销售任务,则商场销售该商品获得的最大利润是多少?
考点:二次函数的应用
专题:
分析:(1)根据题意,直接列出关系式即可解决问题.
(2)运用利润与销售单价、销售量之间的关系,列出函数关系式即可解决问题.
(3)求出销售单价的范围,借助二次函数的性质,即可解决问题.
(2)运用利润与销售单价、销售量之间的关系,列出函数关系式即可解决问题.
(3)求出销售单价的范围,借助二次函数的性质,即可解决问题.
解答:解:(1)y=200+20(80-x)=-20x+1800,
即每星期的销售量y(件)与销售单价x(x<80)(元)之间的函数关系式为:y=-20x+1800.
(2)w=(x-60)(-20x+1800)=-20x2+3000x-108000,
即利润w与销售单价x之间的函数关系式为:w=-20x2+3000x-108000.
(3)由题意得:
,
解得:76≤x≤78.
∵w=-20x2+3000x-108000的图象开口向下,
且对称轴为:x=-
=75,
∴当x=76时,w取得最大值,此时w=-20×762+3000×76-108000=4480(元).
即每星期的销售量y(件)与销售单价x(x<80)(元)之间的函数关系式为:y=-20x+1800.
(2)w=(x-60)(-20x+1800)=-20x2+3000x-108000,
即利润w与销售单价x之间的函数关系式为:w=-20x2+3000x-108000.
(3)由题意得:
|
解得:76≤x≤78.
∵w=-20x2+3000x-108000的图象开口向下,
且对称轴为:x=-
| 3000 |
| 2×(-20) |
∴当x=76时,w取得最大值,此时w=-20×762+3000×76-108000=4480(元).
点评:该题主要考查了二次函数的性质及其应用问题;解题的关键是深入把握题意,正确列出函数关系式,灵活运用有关定理来分析、判断、解答.

练习册系列答案
相关题目
 如图,OC是平角∠AOB的平分线,OD、OE分别是∠AOC和∠BOC的平分线,图中和∠COD互余的角(不含∠COD)的个数是( )
如图,OC是平角∠AOB的平分线,OD、OE分别是∠AOC和∠BOC的平分线,图中和∠COD互余的角(不含∠COD)的个数是( )| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,四边形ABCD中,要使AB∥CD,可添加哪些条件?(不添加辅助线,至少写出3个)
如图,四边形ABCD中,要使AB∥CD,可添加哪些条件?(不添加辅助线,至少写出3个)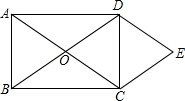 如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.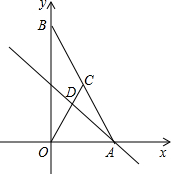 如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(0A<OB)是方程组
如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(0A<OB)是方程组 如图,已知BC>AB,AD=DC,BD平分∠ABC,求证:∠A+∠C=180°.
如图,已知BC>AB,AD=DC,BD平分∠ABC,求证:∠A+∠C=180°.