Question

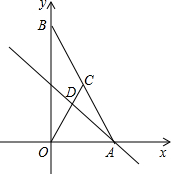如图，在平面直角坐标系中，点A、B分别在x轴、y轴上，线段OA、OB的长（0A＜OB）是方程组

2x=y 3x-y=6

的解，点C是直线y=2x与直线AB的交点，点D在线段OC上，OD=2

5

．
（1）求直线AB的解析式及点C的坐标；
（2）求直线AD的解析式；
（3）在直线AD上是否存在一点P，使△POD与△AOC的面积相等？若存在，请求出点P的坐标；若不存在，请说明理由．

Answer 1

考点：一次函数综合题

专题：

分析：（1）根据解方程组，可得A、B的坐标，根据待定系数法，可得函数解析式，根据解方程组，可得点C的坐标；
（2）根据D在OC上，OD=2

5

，可得方程组，根据解方程组，可得D点坐标，根据待定系数法，可得AD的函数解析式；
（3）根据点到直线的距离，可得关于P到OB的距离，根据三角形的面积相等，可得方程，根据解方程，可得答案．

解答：解：（1）解

2x=y 3x-y=6

，得

x=6 y=12

，即A（6，0）、B（0，12）．
设直线AB的解析式y=kx+b，把A、B点的坐标代入函数解析式，得

6K+b=0 b=12

，
解得

k=-2 b=12

．
直线AB的解析式y=-2x+12，
由点C是直线y=2x与直线AB的交点，得

y=-2x+12 y=2x

，
解得

y=6 x=3

C点的坐标是（3，6）；
（2）由点D在线段OC上，OD=2

5

，
得

x2+y2=20 y=2x

，解得

x=2 y=4

，即D点坐标是（2，4）
设AD的函数解析式为y=kx+b，把A、D点的坐标代入，得

6k+b=0 2k+b=4

，解得

k=-1 b=6

．
AD的函数解析式为y=-x+6；
（3）在直线AD上是存在一点P，使△POD与△AOC的面积相等，
设p（a，-a+6），P到OD的距离是

|2a-(-a+16)|

22+12

=

|3a-16|

5

．
由三角形的面积相等，得

1

2

×2

5

×

|3a-16|

5

=

1

2

×6×6．
|3a-16|=18
解得a₁=

34

3

，a₂=-

2

3

当a=

34

3

时，-a+6=-

16

3

；
当a=-

2

3

时，-a+6=

20

3

；
P₁（

34

3

，-

16

3

），p₂（-

2

3

，

20

3

）．

点评：本题考查了一次函数的综合题，利用了待定系数法求函数解析式，解方程组求交点的坐标，点到直线的距离表示三角形的高，三角形的面积公式．