题目内容
9.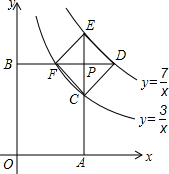 如图,过反比例函数y=$\frac{3}{x}$(x>0)和y=$\frac{7}{x}$(x>0)的图象之间的点P作两坐标轴的垂线,分别交两坐标轴于点A,B,交两函数图象于点C,E,F,D.若四边形OAPB与四边形CDEF都是正方形,则正方形CDEF的面积为$\frac{8}{5}$.
如图,过反比例函数y=$\frac{3}{x}$(x>0)和y=$\frac{7}{x}$(x>0)的图象之间的点P作两坐标轴的垂线,分别交两坐标轴于点A,B,交两函数图象于点C,E,F,D.若四边形OAPB与四边形CDEF都是正方形,则正方形CDEF的面积为$\frac{8}{5}$.
分析 设OA=a,由四边形OAPB是正方形,得到PA=PB=a,由于点C在y=$\frac{3}{x}$的图象上,得出C(a,$\frac{3}{a}$),求得AC=$\frac{3}{a}$,PC=a-$\frac{3}{a}$,由于四边形CDEF是正方形,得到PD=PC=a-$\frac{3}{a}$,由于点D在y=$\frac{7}{x}$(x>0)的图象上,求得D($\frac{7}{a}$,a),得到关于a的方程PD=$\frac{7}{a}$-a=a-$\frac{3}{a}$,解得a=$\sqrt{5}$,结论即可得出.
解答 解:设OA=a,
∵四边形OAPB是正方形,
∴PA=PB=a,
∵点C在y=$\frac{3}{x}$的图象上,
∴C(a,$\frac{3}{a}$),
∴AC=$\frac{3}{a}$,
∴PC=a-$\frac{3}{a}$,
∵四边形CDEF是正方形,
∴PD=PC=a-$\frac{3}{a}$,
∵点D在y=$\frac{7}{x}$(x>0)的图象上,
∴D($\frac{7}{a}$,a),
∴PD=$\frac{7}{a}$-a=a-$\frac{3}{a}$,
∴a=$\sqrt{5}$,
∴DF=$\frac{4}{\sqrt{5}}$,
∴正方形CDEF的面积=$\frac{1}{2}$×$(\frac{4}{\sqrt{5}})^{2}$=$\frac{8}{5}$,
故答案为:$\frac{8}{5}$.
点评 本题考查了反比例函数系数k的几何意义,正方形的性质,正方形面积的求法,正确识别图形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如右:甲:8,7,10,7,8; 乙:9,5,10,9,7.
(1)将下表填写完整;
(2)若你是教练,根据以上信息,你会选择谁参加射击比赛,理由是什么?
(1)将下表填写完整;
| 平 均 数 | 方 差 | |
| 甲 | 8 | 1.2 |
| 乙 | 8 | 3.2 |
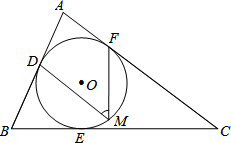 如图,⊙O是△ABC的内切圆,点D、E、F为切点,点M为优弧DEF上任意一点,∠B=66°,∠C=37°,求∠M的大小.
如图,⊙O是△ABC的内切圆,点D、E、F为切点,点M为优弧DEF上任意一点,∠B=66°,∠C=37°,求∠M的大小.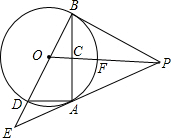 如图,PA为⊙O的切线,A为切点.过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点D,与PA的延长线交于点E.
如图,PA为⊙O的切线,A为切点.过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点D,与PA的延长线交于点E. 某公司投资1200万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本50元,该产品进入市场后不得低于80元/件且不得超过160元/件,该产品销售量y(万件)与产品售价x(元)之间的关系如图所示.
某公司投资1200万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本50元,该产品进入市场后不得低于80元/件且不得超过160元/件,该产品销售量y(万件)与产品售价x(元)之间的关系如图所示.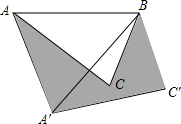 如图,在△ABC中,AB=4,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为4$\sqrt{2}$.
如图,在△ABC中,AB=4,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为4$\sqrt{2}$. 已知关于x的方程mx2-(3m-1)x+2m-2=0.
已知关于x的方程mx2-(3m-1)x+2m-2=0.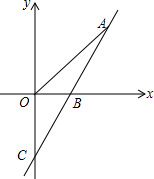 如图,直线y=kx-2与x轴,y轴分别交于点B,C,且OC=2OB,A为直线BC上一动点.
如图,直线y=kx-2与x轴,y轴分别交于点B,C,且OC=2OB,A为直线BC上一动点.