题目内容
4.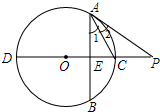 如图,直线CD⊥弦AB,∠1=∠2
如图,直线CD⊥弦AB,∠1=∠2(1)求证:PA为⊙O的切线;
(2)若DE=8,CE=2,求PC的长.
分析 (1)连接OA.欲证明PA为⊙O的切线,只需证明OA⊥AP即可.
(2)根据已知条件求得OE=3,然后根据射影定理求得OP,进而即可求得PC的长.
解答 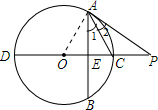 证明:(1)连接OA.
证明:(1)连接OA.
∵OA=OC,
∴∠OCA=∠OAC;
又∵CD⊥弦AB,
∴∠OCA+∠1=90°(直角三角形的两个锐角互余);
又∵∠1=∠2,
∴∠2+∠CAO=90°(等量代换),
∴OA⊥AP,
∵A在⊙O上,
∴PA是⊙O的切线.
(2)∵DE=8,CE=2,
∴DC=10,
∴OD=OC=OA=5,
∴OE=3,
在RT△AOP中,AE⊥OP,
∴AO2=OE•PO,
∴PO=$\frac{O{A}^{2}}{OE}$=$\frac{25}{3}$,
∵PC=PO-OC=$\frac{25}{3}$-5=$\frac{10}{3}$.
点评 本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了射影定理.

练习册系列答案
相关题目
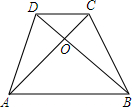 如图,四边形ABCD中,AB∥CD,AC,BD相交于O,△DOC和△BCD的面积比是1:3,则△DOC和△ABD的面积比是1:12.
如图,四边形ABCD中,AB∥CD,AC,BD相交于O,△DOC和△BCD的面积比是1:3,则△DOC和△ABD的面积比是1:12.