题目内容
14.化简求值:$\frac{1}{3}$a-2(a-$\frac{1}{3}$b2)-($\frac{2}{3}$a-$\frac{1}{3}$b2),其中a=3,b=$\frac{2}{3}$.分析 首先去括号,然后再合并同类项把$\frac{1}{3}$a-2(a-$\frac{1}{3}$b2)-($\frac{2}{3}$a-$\frac{1}{3}$b2)化简,再代入a、b的值进行计算即可.
解答 解:原式=$\frac{1}{3}$a-2a+$\frac{2}{3}$b2-$\frac{2}{3}$a+$\frac{1}{3}$b2,
=-$\frac{7}{3}$a+b2,
当a=3,b=$\frac{2}{3}$时,原式=$-\frac{7}{3}$×3+$\frac{4}{9}$=-7+$\frac{4}{9}$=-6$\frac{5}{9}$.
点评 此题主要考查了整式的化简求值,给出整式中字母的值,求整式的值的问题,一般要先化简,再把给定字母的值代入计算,得出整式的值,不能把数值直接代入整式中计算.

练习册系列答案
相关题目
3.下列计算正确的是( )
| A. | |$\root{3}{-4}$|=2 | B. | $\sqrt{49}$=±7 | C. | $\sqrt{(-5)^{2}}$=-5 | D. | $\root{3}{(-\frac{1}{2})^{3}}$=-$\frac{1}{2}$ |
 如图,四边形ABCD为⊙O的内接四边形,若∠ABC=125°,则∠ADC=55度.
如图,四边形ABCD为⊙O的内接四边形,若∠ABC=125°,则∠ADC=55度.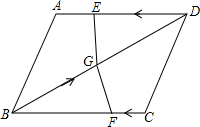 如图,在四边形ABCD中,AD=BC=12,AB=CD,BD=15,点E从D点出发,以每秒4个单位的速度沿D→A→D匀速移动,点F从点C出发,以每秒1个单位的速度沿CB向点B作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.
如图,在四边形ABCD中,AD=BC=12,AB=CD,BD=15,点E从D点出发,以每秒4个单位的速度沿D→A→D匀速移动,点F从点C出发,以每秒1个单位的速度沿CB向点B作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.
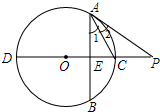 如图,直线CD⊥弦AB,∠1=∠2
如图,直线CD⊥弦AB,∠1=∠2