题目内容
9.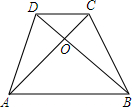 如图,四边形ABCD中,AB∥CD,AC,BD相交于O,△DOC和△BCD的面积比是1:3,则△DOC和△ABD的面积比是1:12.
如图,四边形ABCD中,AB∥CD,AC,BD相交于O,△DOC和△BCD的面积比是1:3,则△DOC和△ABD的面积比是1:12.
分析 由△DOC和△BCD的面积比是1:3,得到$\frac{OD}{BO}$=$\frac{1}{3}$,根据AB∥CD,推出△COD∽△BOA,根据相似三角形的性质得到$\frac{OD}{BO}$=$\frac{OC}{AO}$=$\frac{1}{3}$,$\frac{{S}_{△COD}}{{S}_{△ABO}}$=($\frac{OD}{OB}$)2=$\frac{1}{9}$,于是求得S△AOD=3S△COD,S△AOB=9△COD,得到S△ABD=12S△COD,即可得到结论.
解答 解:∵△DOC和△BCD的面积比是1:3,
∴$\frac{OD}{BO}$=$\frac{1}{3}$,
∵AB∥CD,
∴△COD∽△BOA,
∴$\frac{OD}{BO}$=$\frac{OC}{AO}$=$\frac{1}{3}$,$\frac{{S}_{△COD}}{{S}_{△ABO}}$=($\frac{OD}{OB}$)2=$\frac{1}{9}$,
∴$\frac{{S}_{△COD}}{{S}_{△AOD}}$=$\frac{OC}{OA}$=$\frac{1}{3}$,
∴S△AOD=3S△COD,S△AOB=9△COD,
∴S△ABD=12S△COD,
∴△DOC和△ABD的面积比是1:12,
故答案为:1:12.
点评 本题考查了相似三角形的判定和性质,三角形的面积,知道等高不等底的三角形的面积比等于底的比是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.投掷一枚质地均匀的正方体骰子600次,朝上一面的点数为3的次数大约是( )
| A. | 100次 | B. | 200次 | C. | 300次 | D. | 400次 |
14.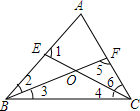 如图所示,在△ABC中,E、F分别在AB、AC上,则下列各式不能成立的是( )
如图所示,在△ABC中,E、F分别在AB、AC上,则下列各式不能成立的是( )
 如图所示,在△ABC中,E、F分别在AB、AC上,则下列各式不能成立的是( )
如图所示,在△ABC中,E、F分别在AB、AC上,则下列各式不能成立的是( )| A. | ∠BOC=∠2+∠6+∠A | B. | ∠2=∠5-∠A | C. | ∠5=∠1+∠A | D. | ∠1=∠ABC+∠4 |
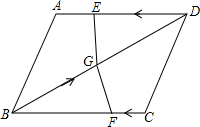 如图,在四边形ABCD中,AD=BC=12,AB=CD,BD=15,点E从D点出发,以每秒4个单位的速度沿D→A→D匀速移动,点F从点C出发,以每秒1个单位的速度沿CB向点B作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.
如图,在四边形ABCD中,AD=BC=12,AB=CD,BD=15,点E从D点出发,以每秒4个单位的速度沿D→A→D匀速移动,点F从点C出发,以每秒1个单位的速度沿CB向点B作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.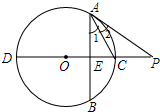 如图,直线CD⊥弦AB,∠1=∠2
如图,直线CD⊥弦AB,∠1=∠2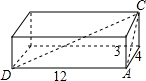 一个长方体盒子,它的长是12dm,宽是4dm,高是3dm,
一个长方体盒子,它的长是12dm,宽是4dm,高是3dm, 有理数a、b、c在数轴上的位置如图所示.化简:|a+c|-|a-b-c|-|b-a|+|b+c|.
有理数a、b、c在数轴上的位置如图所示.化简:|a+c|-|a-b-c|-|b-a|+|b+c|.