题目内容
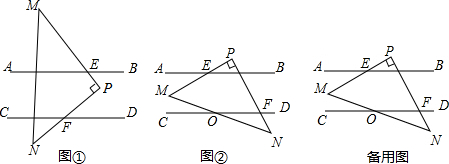
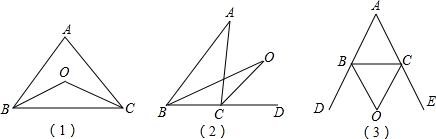
16.如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为∠PFD+∠AEM=90°;
(2)当△PMN所放位置如图②所示时,求证:∠PFD-∠AEM=90°;
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N的度数.
分析 (1)由平行线的性质得出∠PFD=∠1,∠2=∠AEM,即可得出结果;
(2)由平行线的性质得出∠PFD+∠1=180°,再由角的互余关系即可得出结果;
(3)由角的互余关系求出∠PHE,再由平行线的性质得出∠PFC的度数,然后由三角形的外角性质即可得出结论.
解答 解:(1)作PG∥AB,如图①所示: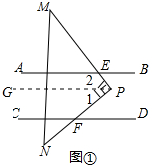
则PG∥CD,
∴∠PFD=∠1,∠2=∠AEM,
∵∠1+∠2=∠P=90°,
∴∠PFD+∠AEM=∠1+∠2=90°,
故答案为:∠PFD+∠AEM=90°;
(2)证明:如图②所示:
∵AB∥CD,
∴∠PFD+∠BHF=180°,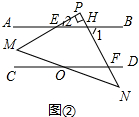
∵∠P=90°,
∴∠BHF+∠2=90°,
∵∠2=∠AEM,
∴∠BHF=∠PHE=90°-∠AEM,
∴∠PFD+90°-∠AEM=180°,
∴∠PFD-∠AEM=90°;
(3)如图③所示: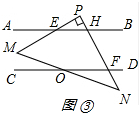
∵∠P=90°,
∴∠PHE=90°-∠FEB=90°-15°=75°,
∵AB∥CD,
∴∠PFC=∠PHE=75°,
∵∠PFC=∠N+∠DON,
∴∠N=75°-30°=45°.
点评 本题考查了平行线的性质、角的互余关系;熟练掌握平行线的性质,弄清角之间的数量关系是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.如果一个三角形的底边长为2x2y+xy-y2,底边上的高为6xy,那么这个三角形的面积为( )
| A. | 6x3y2+3x2y2-3xy3 | B. | 6x2y2+3xy-3xy2 | ||
| C. | 6x2y2+3x2y2-y2 | D. | 6x2y+3x2y2 |
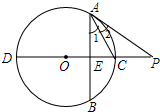 如图,直线CD⊥弦AB,∠1=∠2
如图,直线CD⊥弦AB,∠1=∠2 如图,⊙O的半径为3cm,A,B,C,D是⊙O上的四个点,AB=AC,AD与BC相交于点E,AE=2cm,ED=2.5cm.
如图,⊙O的半径为3cm,A,B,C,D是⊙O上的四个点,AB=AC,AD与BC相交于点E,AE=2cm,ED=2.5cm.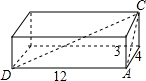 一个长方体盒子,它的长是12dm,宽是4dm,高是3dm,
一个长方体盒子,它的长是12dm,宽是4dm,高是3dm, 如图所示,点C是线段AB上的点,点D是线段BC的中点,点E是线段AB的中点,若AB=12,AC=8,则ED=4.
如图所示,点C是线段AB上的点,点D是线段BC的中点,点E是线段AB的中点,若AB=12,AC=8,则ED=4.