题目内容
19.一根钢筋三脚架的三边分别为20cm,50cm,60cm,现要做一个与其相似的钢筋三脚架,要求以其中一根为一边,从另一根上截下两段(允许有余料)作为另外两边,则不同的截法有( )| A. | 一种 | B. | 两种 | C. | 三种 | D. | 五种 |
分析 当20cm为一边,设截取的另外两边长分别为xcm,ycm,若20为最长边,则当$\frac{20}{x}$=$\frac{50}{y}$=$\frac{60}{20}$时,两三角形相似,解得x=$\frac{20}{3}$,y=$\frac{50}{3}$,由于x+y=$\frac{70}{3}$,于是可把50cm截取两段或把60cm截取两段;当20为与50的对应边,则当$\frac{20}{x}$=$\frac{50}{20}$=$\frac{60}{y}$,两三角形相似,解得x=8,y=24,于是可把50cm截取两段或把60cm截取两段;当取50cm为一边,设截取的另外两边长分别为acm,acm,则当$\frac{20}{a}$=$\frac{50}{b}$=$\frac{60}{50}$时两三角形相似,解得a=$\frac{50}{3}$,b=$\frac{125}{3}$,于是可把60cm截取两段.
解答 解:取20cm为一边,设截取的另外两边长分别为xcm,ycm,
当$\frac{20}{x}$=$\frac{50}{y}$=$\frac{60}{20}$,解得x=$\frac{20}{3}$,y=$\frac{50}{3}$,所以x+y=$\frac{70}{3}$,则20<x+y<50,所以可把50cm截取两段或把60cm截取两段;
当$\frac{20}{x}$=$\frac{50}{20}$=$\frac{60}{y}$,解得x=8,y=24,所以x+y=32,则20<x+y<50,所以可把50cm截取两段或把60cm截取两段;
取50cm为一边,设截取的另外两边长分别为acm,acm,
当$\frac{20}{a}$=$\frac{50}{b}$=$\frac{60}{50}$,解得a=$\frac{50}{3}$,b=$\frac{125}{3}$,所以a+b=$\frac{175}{3}$,则50<a+b<60,所以可把60cm截取两段.
共有5种可能的截法.
点评 本题考查了相似三角形的判定:三组对应边的比相等的两个三角形相似.本题的关键是运用分类讨论的思想解决问题.

 阅读快车系列答案
阅读快车系列答案| A. | 6x3y2+3x2y2-3xy3 | B. | 6x2y2+3xy-3xy2 | ||
| C. | 6x2y2+3x2y2-y2 | D. | 6x2y+3x2y2 |
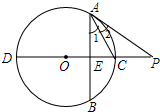 如图,直线CD⊥弦AB,∠1=∠2
如图,直线CD⊥弦AB,∠1=∠2 如图,⊙O的半径为3cm,A,B,C,D是⊙O上的四个点,AB=AC,AD与BC相交于点E,AE=2cm,ED=2.5cm.
如图,⊙O的半径为3cm,A,B,C,D是⊙O上的四个点,AB=AC,AD与BC相交于点E,AE=2cm,ED=2.5cm. 如图所示,点C是线段AB上的点,点D是线段BC的中点,点E是线段AB的中点,若AB=12,AC=8,则ED=4.
如图所示,点C是线段AB上的点,点D是线段BC的中点,点E是线段AB的中点,若AB=12,AC=8,则ED=4.