题目内容
 如图,△ABC的边AB=3,AC=2,Ⅰ、Ⅱ、Ⅲ分别表示以AB、AC、BC为边的正方形,求图中三个阴影部分的面积之和的最大值为
如图,△ABC的边AB=3,AC=2,Ⅰ、Ⅱ、Ⅲ分别表示以AB、AC、BC为边的正方形,求图中三个阴影部分的面积之和的最大值为考点:全等三角形的判定与性质,正方形的性质
专题:
分析:把△CFH绕点C顺时针旋转90°得到△BCH′,然后判断出A、C、H′三点共线,再根据等底等高的三角形的面积相等可得S△BCH′=S△ABC,即S△CFH=S△ABC,同理可得S△BDG=S△ABC,S△AEM=S△ABC,从而得到阴影部分的面积的和=3S△ABC,再根据三角形的面积公式,当AB⊥AC时,面积最大列式计算即可得解.
解答: 解:如图,把△CFH绕点C顺时针旋转90°得到△BCH′,
解:如图,把△CFH绕点C顺时针旋转90°得到△BCH′,
∵Ⅱ表示正方形,
∴AC=CH=CH′,∠ACH+∠BCH′=360°-90°×2=180°,
∴A、C、H′三点共线,
∴S△BCH′=S△ABC,
∴S△CFH=S△ABC,
同理可得S△BDG=S△ABC,S△AEM=S△ABC,
∴阴影部分的面积的和=3S△ABC,
∵AB=3,AC=2,
∴当AB⊥AC时,△ABC的面积最大,最大值为S△ABC=
AB•AC=
×3×2=3,
∴三个阴影部分的面积之和的最大值为3×3=9.
故答案为:9.
 解:如图,把△CFH绕点C顺时针旋转90°得到△BCH′,
解:如图,把△CFH绕点C顺时针旋转90°得到△BCH′,∵Ⅱ表示正方形,
∴AC=CH=CH′,∠ACH+∠BCH′=360°-90°×2=180°,
∴A、C、H′三点共线,
∴S△BCH′=S△ABC,
∴S△CFH=S△ABC,
同理可得S△BDG=S△ABC,S△AEM=S△ABC,
∴阴影部分的面积的和=3S△ABC,
∵AB=3,AC=2,
∴当AB⊥AC时,△ABC的面积最大,最大值为S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴三个阴影部分的面积之和的最大值为3×3=9.
故答案为:9.
点评:本题考查了正方形的性质,旋转变换的性质,利用旋转的性质作辅助线判断出每一个阴影部分的面积等于△ABC的面积是解题的关键,也是本题的难点.

练习册系列答案
相关题目
下列运算中正确的是( )
| A、a2+a3=a5 | ||
B、
| ||
| C、(2a)3=6a3 | ||
| D、-(3x-2)(-3x-2)=4-9x2 |

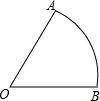 如图,扇形OAB的圆心角为2α,点P为弧AB上一点,将此扇形翻折,当点O和点P重合时折痕恰巧过点B,且
如图,扇形OAB的圆心角为2α,点P为弧AB上一点,将此扇形翻折,当点O和点P重合时折痕恰巧过点B,且 已知如图,∠ACB=90°,
已知如图,∠ACB=90°,