题目内容
将抛物线y=x2+x向右平移1个单位后,所得新抛物线的表达式是 .
考点:二次函数图象与几何变换
专题:
分析:先把函数化为顶点式的形式,再根据“左加右减”的法则即可得出结论.
解答:解:∵抛物线y=x2+x可化为y=(x+
)2-
,
∴抛物线向右平移1个单位后,所得新抛物线的表达式为y=(x+
-1)2-
,即y=x2-x.
故答案为:y=x2-x.
| 1 |
| 2 |
| 1 |
| 4 |
∴抛物线向右平移1个单位后,所得新抛物线的表达式为y=(x+
| 1 |
| 2 |
| 1 |
| 4 |
故答案为:y=x2-x.
点评:本题考查的是二次函数的图象与几何变换,熟知“上加下减,左加右减”的法则是解答此题的关键.

练习册系列答案
相关题目
下列图案中,是中心对称又是轴对称的图形是( )
A、 |
B、 |
C、 |
D、 |

 如图,在平面直角坐标系xOy中,点A的坐标为(1,
如图,在平面直角坐标系xOy中,点A的坐标为(1,
 如图,△ABC的边AB=3,AC=2,Ⅰ、Ⅱ、Ⅲ分别表示以AB、AC、BC为边的正方形,求图中三个阴影部分的面积之和的最大值为
如图,△ABC的边AB=3,AC=2,Ⅰ、Ⅱ、Ⅲ分别表示以AB、AC、BC为边的正方形,求图中三个阴影部分的面积之和的最大值为 如图,在平面直角坐标系中,点A、B分别在x轴、y轴的正半轴上,点B的坐标是(0,7),且AB=25.△AOB绕某点旋转180°后,点C(36,9)是点B的对应点.
如图,在平面直角坐标系中,点A、B分别在x轴、y轴的正半轴上,点B的坐标是(0,7),且AB=25.△AOB绕某点旋转180°后,点C(36,9)是点B的对应点.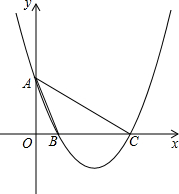 如图,抛物线y=ax2+bx+4与y轴交于点A,与x轴交于点B,C两点,∠ABO=∠OAC,OB:BC=1:3.
如图,抛物线y=ax2+bx+4与y轴交于点A,与x轴交于点B,C两点,∠ABO=∠OAC,OB:BC=1:3.