题目内容
 已知如图,∠ACB=90°,
已知如图,∠ACB=90°,| AC |
| BC |
| 4 |
| 3 |
考点:勾股定理
专题:
分析:根据AC和BC的比值以及勾股定理可求出AC,BC的长,再利用射影定理即可求出AD的长.
解答:解:∵∠ACB=90°,
∴AC2+BC2=AB2,
∵
=
,AB=15cm,
∴AC=12,BC=9,
∵CD⊥AB,D是垂足,
∴AC2=AD•AB,
∴AD=
.
∴AC2+BC2=AB2,
∵
| AC |
| BC |
| 4 |
| 3 |
∴AC=12,BC=9,
∵CD⊥AB,D是垂足,
∴AC2=AD•AB,
∴AD=
| 36 |
| 5 |
点评:本题考查了勾股定理和射影定理的运用,解题的关键是利用线段之间的比值和勾股定理求出AC,BC的长.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 在某水果店一次性购买A种水果的单价y(元)与购买量x(千克)的函数关系如图.
在某水果店一次性购买A种水果的单价y(元)与购买量x(千克)的函数关系如图.
 如图,△ABC的边AB=3,AC=2,Ⅰ、Ⅱ、Ⅲ分别表示以AB、AC、BC为边的正方形,求图中三个阴影部分的面积之和的最大值为
如图,△ABC的边AB=3,AC=2,Ⅰ、Ⅱ、Ⅲ分别表示以AB、AC、BC为边的正方形,求图中三个阴影部分的面积之和的最大值为 如图,直线y=4x+4与x轴、y轴相交于B、C两点,抛物线y=ax2-2ax+c(a≠0)过点B、C,且与x轴另一个交点为A,以OC、OA为边作矩形OADC,CD交抛物线于点G.
如图,直线y=4x+4与x轴、y轴相交于B、C两点,抛物线y=ax2-2ax+c(a≠0)过点B、C,且与x轴另一个交点为A,以OC、OA为边作矩形OADC,CD交抛物线于点G. 如图,在平面直角坐标系中,点A、B分别在x轴、y轴的正半轴上,点B的坐标是(0,7),且AB=25.△AOB绕某点旋转180°后,点C(36,9)是点B的对应点.
如图,在平面直角坐标系中,点A、B分别在x轴、y轴的正半轴上,点B的坐标是(0,7),且AB=25.△AOB绕某点旋转180°后,点C(36,9)是点B的对应点.
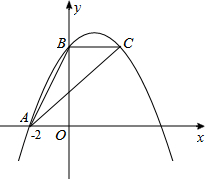 如图,抛物线y=-
如图,抛物线y=-