Question

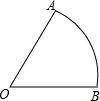如图，扇形OAB的圆心角为2α，点P为弧AB上一点，将此扇形翻折，当点O和点P重合时折痕恰巧过点B，且

AB

PB

=

6

5

，则α的正切值为

 

．

Answer 1

考点：翻折变换（折叠问题）

专题：计算题

分析：BE为折痕作OC⊥AB于C，交弧AB于D，设AB=6t，PB=5t，根据折叠的性质得BP=BO=5t，由于OC⊥AB，根据垂径定理得AC=BC=

1

2

AB=3t，弧AD=弧BD，则∠BOD=

1

2

∠AOB=α，在Rt△BOC中，先根据勾股定理计算出OC=4t，然后根据正切的定义求解．

解答：解：BE为折痕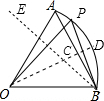，作OC⊥AB于C，交弧AB于D，如图，
∵

AB

PB

=

6

5

，
∴设AB=6t，PB=5t，
∵点O和点P重合时折痕恰巧过点B，
∴BP=BO=5t，
∵OC⊥AB，
∴AC=BC=

1

2

AB=3t，弧AD=弧BD，
∴∠BOD=

1

2

∠AOB=

1

2

•2α=α，
在Rt△BOC中，OC=

OB2-BC2

=4t，
∴tan∠BOC=

BC

OC

=

3t

4t

=

3

4

．
即tanα=

3

4

．
故答案为

3

4

．

点评：本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了勾股定理、垂径定理和正切的定义．