Question

18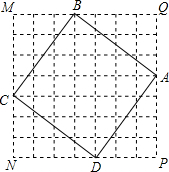．如图，在正方形网格MNPQ中，每个小方格的边长都相等，四边形ABCD的顶点在正方形MNPQ的4条边的小方格顶点上．
（1）设正方形MNPQ网格内的每个小方格的边长为1．
①判断四边形ABCD的形状，并说明理由．
②求四边形ABCD的面积；
（2）设MB=a，BQ=b，利用这个图形中的直角三角形和正方形的面积关系，你能验证已学过的一个学公式或定理吗？

Answer 1

分析 （1）①根据正方形的判定即可得出结果；
②由题意得出S_{正方形ABCD}=S_{正方形MNPQ}-4S_△ABQ，即可得出结果；
（2）显然根据面积能够验证勾股定理以及完全平方公式．

解答 解：（1）①四边形ABCD是正方形．
理由是：在△BMC和△CND中，
$\left\{\begin{array}{l}{MC=ND=4}\\{∠M=∠N=90°}\\{MB=CN=3}\end{array}\right.$，
∴△BMC≌△CND，
∴BC=CD，∠MBC=∠NCD，
∵∠MBC+∠MCB=90°，
∴∠NCD+∠MBC=90°，
∴∠BCD=180°-（∠NCD+∠MBC）=90°，
同理可证：BC=AD=AB，
∴四边形ABCD是正方形．
②∵MQ=7，
∴S_{正方形MNPQ}=7²=49．
∴S_{正方形ABCD}=S_{正方形MNPQ}-4S_△ABQ=49-4×6=25．
（2）验证勾股定理或完全平方公式．
验证：在△BCM和△ABQ中，
$\left\{\begin{array}{l}{BM=AQ}\\{∠M=∠Q}\\{CM=BQ}\end{array}\right.$，
∴△BCM≌△ABQ（SAS），
同理△CDN≌△DAP≌△BCM．
∵MB=a，BQ=b，S_{正方形MNPQ}=S_{正方形ABCD}+4S_△ABQ，
∴（a+b）²=a²+b²+4×$\frac{1}{2}$ab，
即（a+b）²=a²+2ab+b²（完全平方公式），
或又∵S_{正方形ABCD}=S_{正方形MNPQ}-4S_△ABQ，
∴AB²=（a+b）²-4×$\frac{1}{2}$ab，即AB²=a²+b²．
设AB=c，得c²=a²+b²（勾股定理）．

点评 本题考查了勾股定理的证明、正方形的判定和性质以及面积的计算、三角形面积的计算、完全平方公式；掌握正方形和三角形面积的计算方法是解决问题的关键．