题目内容
 如图,直线AB,CD交于点O,OE是一条射线.
如图,直线AB,CD交于点O,OE是一条射线.(1)写出图中所有的对顶角和邻补角;
(2)若∠AOC=40°,OE平分∠BOC,求∠DOE的度数.
考点:对顶角、邻补角
专题:
分析:(1)根据对顶角是一个角的两边是另一个角两边的反向延长线,邻补角是两个角有一条公共边,另一条边互为反向延长线,可得答案;
(2)根据邻补角互补,可得∠BOC的度数,根据角平分线的性质,可得∠COE的度数,再根据邻补角互补,可得答案.
(2)根据邻补角互补,可得∠BOC的度数,根据角平分线的性质,可得∠COE的度数,再根据邻补角互补,可得答案.
解答:解:(1)图中的对顶角有∠AOC与∠BOD;∠BOC与∠AOD;
图中的邻补角有∠AOC与∠BOC,∠BOC与∠BOD,∠BOD与∠AOD,∠AOD与∠AOC,∠AOE与∠BOE,∠COE与∠DOE;
(2)由邻补角互补,得∠BOC=180°-∠AOC=180°-40°=140°,
由OE平分∠BOC,得∠COE=
∠BOE=
×140°=70°,
由邻补角互补,得∠DOE=180°-∠COE=180°-70°=110°.
图中的邻补角有∠AOC与∠BOC,∠BOC与∠BOD,∠BOD与∠AOD,∠AOD与∠AOC,∠AOE与∠BOE,∠COE与∠DOE;
(2)由邻补角互补,得∠BOC=180°-∠AOC=180°-40°=140°,
由OE平分∠BOC,得∠COE=
| 1 |
| 2 |
| 1 |
| 2 |
由邻补角互补,得∠DOE=180°-∠COE=180°-70°=110°.
点评:本题考查了对顶角与邻补角,利用了邻补角的性质,角平分线的性质.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
观察如图所示前三个图形及数的规律,则第四个□的数是 ( )


A、
| ||||
| B、3 | ||||
C、
| ||||
D、
|

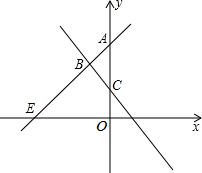 直线y=kx+4(k≠0)与y=-2x+1交于点B,若S△ABC=
直线y=kx+4(k≠0)与y=-2x+1交于点B,若S△ABC=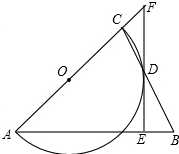 如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.
如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F. 如图,AD是△ABC的BC边上的中线,若AB=2,AC=1,求AD的取值范围.
如图,AD是△ABC的BC边上的中线,若AB=2,AC=1,求AD的取值范围. 如图,在Rt△ABC中,已知∠ACB=90°,AC=m,∠BAC=α,求Rt△ABC的面积.
如图,在Rt△ABC中,已知∠ACB=90°,AC=m,∠BAC=α,求Rt△ABC的面积.