Question

如图，AD是△ABC的BC边上的中线，若AB=2，AC=1，求AD的取值范围．

Answer 1

考点：三角形三边关系,全等三角形的判定与性质

专题：

分析：延长AD到E，使AD=DE，连接BE，证△ADC≌△EDB，推出EB=AC，根据三角形的三边关系定理求出即可．

解答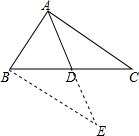：解：延长AD到E，使AD=DE，连接BE，
∵AD是△ABC的中线，
∴BD=CD，
在△ADC与△EDB中，

BD=CD ; ∠ADC=∠BDE AD=DE

，
∴△ADC≌△EDB（SAS），
∴EB=AC，
根据三角形的三边关系定理：2-1＜AE＜2+1，
∴0.5＜AD＜1.5，
故AD的取值范围为0.5＜AD＜1.5．

点评：本题主要考查对全等三角形的性质和判定，三角形的三边关系定理等知识点的理解和掌握，能推出2-1＜2AD＜2+1是解此题的关键．