题目内容
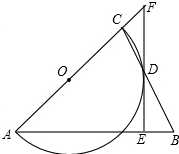 如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.
如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为2,BE=1,求
| AE |
| AF |
考点:切线的判定
专题:
分析:(1)连接OD,可证明OD∥AB,可得OD⊥DE,可得出结论;
(2)连接AD,在Rt△ADB中可求得DE,再根据OD∥AB,利用平行线分线段成比例求得FD,进一步可求得
.
(2)连接AD,在Rt△ADB中可求得DE,再根据OD∥AB,利用平行线分线段成比例求得FD,进一步可求得
| AE |
| AF |
解答:(1)证明:
如图1,连接OD,

∵OC=OD,
∴∠OCD=∠ODC,
∵AB=AC,
∴∠ACB=∠B,
∴∠ODC=∠B,
∴OD∥AB,
∵DE⊥AB,
∴DE⊥OD,
∴DE是⊙O的切线;
(2)解:如图2,连接AD,
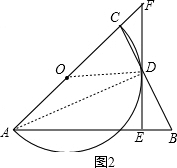
∵AC为直径,
∴AD⊥BC,
∵半径为2,BE=1,
∴OD=2,AB=AC=4,AE=AB-BE=3,
∵DE⊥AB,
∴DE2=AE•BE=3,解得DE=
,
又OD∥AB,
∴
=
,即
=
,
∴
=
,解得DF=2
,
在Rt△ODF中,可求得OF=4,
又
=
,
∴
=
=
=
.
如图1,连接OD,

∵OC=OD,
∴∠OCD=∠ODC,
∵AB=AC,
∴∠ACB=∠B,
∴∠ODC=∠B,
∴OD∥AB,
∵DE⊥AB,
∴DE⊥OD,
∴DE是⊙O的切线;
(2)解:如图2,连接AD,

∵AC为直径,
∴AD⊥BC,
∵半径为2,BE=1,
∴OD=2,AB=AC=4,AE=AB-BE=3,
∵DE⊥AB,
∴DE2=AE•BE=3,解得DE=
| 3 |
又OD∥AB,
∴
| DF |
| EF |
| OD |
| AE |
| DF |
| DF+DE |
| OD |
| AE |
∴
| DF | ||
DF+
|
| 2 |
| 3 |
| 3 |
在Rt△ODF中,可求得OF=4,
又
| OF |
| AF |
| OD |
| AE |
∴
| AE |
| AF |
| OD |
| OF |
| 2 |
| 4 |
| 1 |
| 2 |
点评:本题主要考查切线的判定和性质及等腰三角形的性质、平行线分线段成比例,掌握切线的证明方法,即有切点时连接圆心和切点证明垂直是解题的关键,注意等腰三角形“三线合一”性质的应用.

练习册系列答案
相关题目
 如图,在△ABC中,分别以AB、AC为边作等边△ABD与等边△ACE,连接BE、CD,BE的延长线与CD交于点F,连接AF,有以下四个结论:
如图,在△ABC中,分别以AB、AC为边作等边△ABD与等边△ACE,连接BE、CD,BE的延长线与CD交于点F,连接AF,有以下四个结论: 如图,直线AB,CD交于点O,OE是一条射线.
如图,直线AB,CD交于点O,OE是一条射线. 如图,在△ABC中,BP、CP分别是△ABC的外角∠DBC和∠ECB的平分线.
如图,在△ABC中,BP、CP分别是△ABC的外角∠DBC和∠ECB的平分线. 如图,CD为等边三角形ABC的高,点O在DC的延长线上,且OD=11,CD=6,⊙O的半径为1,若将⊙O绕点C按顺时针方向旋转360°,在旋转过程中,⊙O与等边三角形ABC的边只有一个公共点的情况一共出现( )
如图,CD为等边三角形ABC的高,点O在DC的延长线上,且OD=11,CD=6,⊙O的半径为1,若将⊙O绕点C按顺时针方向旋转360°,在旋转过程中,⊙O与等边三角形ABC的边只有一个公共点的情况一共出现( ) 圆锥形的烟囱帽的底面直径是80cm,母线长为50cm.
圆锥形的烟囱帽的底面直径是80cm,母线长为50cm.