题目内容
15．如图，是一个正六棱柱的主视图和左视图，则图中的a=（ ）
| A． | $\sqrt{3}$ | B． | 2$\sqrt{3}$ | C． | 2 | D． | 1 |
分析 由正六棱柱的主视图和左视图，可得到正六棱柱的边长为2，求a的值可结合俯视图来解答．
解答 
解：由正六棱柱的主视图和左视图，可得到正六棱柱的最长的对角线长是4，则边长为2，
作AD⊥BC于D，在△ABC中，AB=AC=2，∠BAC=120°，
∴在直角△ABD中，∠ABD=30°，AD=1，
∴a=BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$．
故选A．
点评 本题考查了正六棱柱的三视图，注意题目中的隐含条件及左视图的特点，可将其转化到直角三角形中解答．培养了学生的空间想象能力．
练习册系列答案
相关题目
如图，菱形ABCD中，分别延长DC，BC至点E，F，使CE=CD，CF=CB，联结DB，BE，EF，FD．
6．
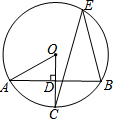如图，A，B，E为⊙O上的点，⊙O的半径OC⊥AB于点D，若∠CEB=30°，OD=1，则AB的长为（ ）
如图，A，B，E为⊙O上的点，⊙O的半径OC⊥AB于点D，若∠CEB=30°，OD=1，则AB的长为（ ）| A． | $\sqrt{3}$ | B． | 4 | C． | 2$\sqrt{3}$ | D． | 6 |
3．如果等腰三角形的两边长分别是方程x2-10x+21=0的两根，那么它的周长为（ ）
| A． | 17 | B． | 15 | C． | 13 | D． | 13或17 |
10．在所给的π，0，-1，$\sqrt{2}$这四个数中，最小的数是（ ）
| A． | π | B． | 0 | C． | -1 | D． | $\sqrt{2}$ |
尺规作图：小明作业本上画的三角形被墨迹污染，他想画出一个与原来完全一样的三角形，请帮助小明想办法用尺规作图画一个出来，并说明你的理由．
7．
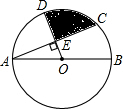如图，⊙O的直径AB=4cm，AC是⊙O的弦，∠BAC=30°，点D在⊙O上，OD⊥AC于E，则阴影部分的面积为（ ）
如图，⊙O的直径AB=4cm，AC是⊙O的弦，∠BAC=30°，点D在⊙O上，OD⊥AC于E，则阴影部分的面积为（ ）| A． | $\frac{20π-15\sqrt{3}}{30}$cm2 | B． | $\frac{24π-15\sqrt{3}}{30}$cm2 | C． | $\frac{20π-18\sqrt{3}}{30}$cm2 | D． | $\frac{20π-15\sqrt{3}}{20}$cm2 |
4．“黑洞”是恒星演化的最后阶段．根据有关理论，当一颗恒星衰老时，其中心的燃料（氢）已经被耗尽，在外壳的重压之下，核心开始坍缩，直到最后形成体积小、密度大的星体．如果这一星体的质量超过太阳质量的三倍，那么就会引发另一次大坍缩．当这种收缩使得它的半径达到施瓦氏（Schwarzschild）半径后，其引力就会变得相当强大，以至于光也不能逃脱出来，从而成为一个看不见的星体--黑洞．施瓦氏半径（单位：米）的计算公式是R=$\frac{2GM}{{c}^{2}}$，其中G=6.67×10-11牛•米2/千克2，为万有引力常数；M表示星球的质量（单位：千克）；c=3×108米/秒，为光在真空中的速度．已知太阳的质量为2×1030千克，则可计算出太阳的施瓦氏半径为（ ）
| A． | 2.96×102米 | B． | 2.96×103米 | C． | 2.96×104米 | D． | 2.96×105米 |