题目内容
11. 如图,点A,C,D在同一条直线上,BC与AE交于点F,AE=AC,AD=BC,FA=FC.求证:∠B=∠D.
如图,点A,C,D在同一条直线上,BC与AE交于点F,AE=AC,AD=BC,FA=FC.求证:∠B=∠D.
分析 根据三角形全等得到对应角相等即可得出结论.
解答 证明:∵FA=FC,
∴∠FAC=∠FCA,
在△ABC和△EDA中,
$\left\{\begin{array}{l}{BC=DA}\\{∠ACB=∠EAD}\\{AC=EA}\end{array}\right.$,
∴△ABC≌△EDA,
∴∠B=∠D.
点评 本题考查了全等三角形的判定与性质,找准对应边和对应角是解题的关键.

练习册系列答案
相关题目
6.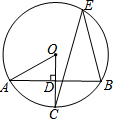 如图,A,B,E为⊙O上的点,⊙O的半径OC⊥AB于点D,若∠CEB=30°,OD=1,则AB的长为( )
如图,A,B,E为⊙O上的点,⊙O的半径OC⊥AB于点D,若∠CEB=30°,OD=1,则AB的长为( )
 如图,A,B,E为⊙O上的点,⊙O的半径OC⊥AB于点D,若∠CEB=30°,OD=1,则AB的长为( )
如图,A,B,E为⊙O上的点,⊙O的半径OC⊥AB于点D,若∠CEB=30°,OD=1,则AB的长为( )| A. | $\sqrt{3}$ | B. | 4 | C. | 2$\sqrt{3}$ | D. | 6 |
3.如果等腰三角形的两边长分别是方程x2-10x+21=0的两根,那么它的周长为( )
| A. | 17 | B. | 15 | C. | 13 | D. | 13或17 |
1.在Rt△ABC中,∠C=90°,若$cosB=\frac{3}{5}$,则sinB的值得是( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
 尺规作图:小明作业本上画的三角形被墨迹污染,他想画出一个与原来完全一样的三角形,请帮助小明想办法用尺规作图画一个出来,并说明你的理由.
尺规作图:小明作业本上画的三角形被墨迹污染,他想画出一个与原来完全一样的三角形,请帮助小明想办法用尺规作图画一个出来,并说明你的理由.