题目内容
8.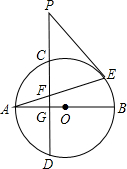 如图,⊙O的直径为AB,弦CD⊥AB于G,PE切⊙O于E交DC延长线于点P,AE交PD于点F.求证:
如图,⊙O的直径为AB,弦CD⊥AB于G,PE切⊙O于E交DC延长线于点P,AE交PD于点F.求证:(1)PE=PF;
(2)PF2=PC•PD.
分析 (1)连接OE,根据切线的性质和圆的半径相等推导即可;
(2)由切割线定理和等量代换可得答案.
解答 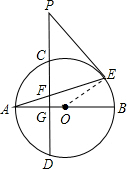 证明(1)连接OE,
证明(1)连接OE,
∵PE为⊙O的切线,
∴∠OED=90°,即∠OEA+∠GFA=90°,
∵CD⊥AB,∴∠FGA=90°,即∠OAE+∠PEF=90°,
∵OA=OE,
∠OAE=∠OEA,
∴∠AFG=∠PEF,
又∠AFG=∠PFE,
∴∠PFE=∠PEF,
∴PE=PF;
(2)根据切割线定理,PE2=PC•PD,
又PE=PF,
∴PF2=PC•PD.
点评 本题考查的是切线的性质,掌握圆的切线垂直于过切点的半径是解题的关键,运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.如果等腰三角形的两边长分别是方程x2-10x+21=0的两根,那么它的周长为( )
| A. | 17 | B. | 15 | C. | 13 | D. | 13或17 |
13.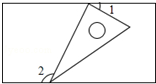 如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=25°,则∠2的度数是( )
如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=25°,则∠2的度数是( )
 如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=25°,则∠2的度数是( )
如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=25°,则∠2的度数是( )| A. | 155° | B. | 135° | C. | 125° | D. | 115° |
18.如果两圆的半径长分别为3cm和5cm,圆心距为7cm,那么这两个圆的位置关系是( )
| A. | 内切 | B. | 外切 | C. | 外离 | D. | 相交 |
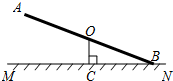 如图,O为跷跷板AB的中点,支柱OC与地面MN垂直,垂足为点C,且OC=50cm,当跷跷板的一端B着地时,另一端A离地面的高度为100cm.
如图,O为跷跷板AB的中点,支柱OC与地面MN垂直,垂足为点C,且OC=50cm,当跷跷板的一端B着地时,另一端A离地面的高度为100cm. 尺规作图:小明作业本上画的三角形被墨迹污染,他想画出一个与原来完全一样的三角形,请帮助小明想办法用尺规作图画一个出来,并说明你的理由.
尺规作图:小明作业本上画的三角形被墨迹污染,他想画出一个与原来完全一样的三角形,请帮助小明想办法用尺规作图画一个出来,并说明你的理由.