题目内容
15.平面直角坐标系中,直线y=2x-4和y=-3x+1交于一点(1,-2),则方程组$\left\{\begin{array}{l}{2x-y=4}\\{3x+y=1}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$.分析 根据两条直线的交点坐标应该是联立两个一次函数解析式所组方程组的解即可直接得到答案.
解答 解:∵直线y=2x-4和直线y=-3x+1交于一点(1,-2),
∴方程组$\left\{\begin{array}{l}{2x-y=4}\\{3x+y=1}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$,
故答案为:$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$.
点评 本题考查了一次函数与二元一次方程组,关键是掌握一次函数与方程组的关系.

练习册系列答案
相关题目
5.下列各组数据中的三个数,可作为三边长构成直角三角形的是( )
| A. | 0.2,0.3,0.4 | B. | 1,1,2 | C. | 6,6,6 | D. | 3,4,5 |
20.将二次函数y=2x2-4x-1的图象向右平移3个单位,则平移后的二次函数的顶点是( )
| A. | (-2,-3) | B. | (4,3) | C. | (4,-3) | D. | (1,0) |
4.整数m满足$\left\{\begin{array}{l}{2m-1>0}\\{4-2m>-1}\end{array}\right.$,则关于x的方程m2x2-4x-2=(m+2)x2+3x+4的解为( )
| A. | x1=-2,x2=-$\frac{3}{2}$ | B. | x1=2,x2=$\frac{3}{2}$ | ||
| C. | x1=-$\frac{6}{7}$ | D. | x1=-2,x2=-$\frac{3}{2}$,x3=-$\frac{6}{7}$ |
5.一个几何体从三个方向看得到的图形如图所示,则这个几何体是( )


| A. | 圆柱 | B. | 圆锥 | C. | 长方体 | D. | 正方体 |
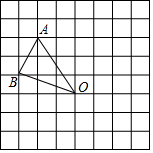 在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABO的三个顶点都在格点上.
在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABO的三个顶点都在格点上. 如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=42°,则∠ACD的度数为83°.
如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=42°,则∠ACD的度数为83°.