题目内容
7.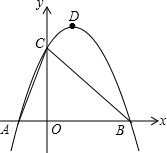 已知:如图,抛物线y=ax2+bx+3交x轴于A(-1,0),B(3,0)两点,交y轴于点C,点D为抛物线的顶点,连接AC,BC.
已知:如图,抛物线y=ax2+bx+3交x轴于A(-1,0),B(3,0)两点,交y轴于点C,点D为抛物线的顶点,连接AC,BC.(1)求抛物线的解析式;
(2)连接BD,求∠DBC的正切值;
(3)点P是线段CB上一动点,过点P作BC的垂线交直线BD于点E,直线PE交直线AC于Q,交第一象限内的抛物线于点M,过点M作x轴的平行线与射线AC交于点G,交y轴于点H,当AQ=GQ时,求点M坐标.
分析 (1)将A,B两点的坐标代入y=ax2+bx+3,得到关于a,b的二元一次方程组,解方程组即可;
(2)利用配方法求出顶点D的坐标,再根据勾股定理的逆定理得出△BCD是直角三角形,然后利用三角函数定义求出∠DBC的正切值;
(3)作出图形,利用待定系数法求出直线AC的解析式为y=3x+3,可设Q点坐标为(a,3a+3),由Q是AG的中点,得出点G纵坐标为6a+6,点M坐标为(4a+3,6a+6),根据点M是抛物线上的点即可求得a的值,进而求出点M坐标.
解答 解:(1)∵抛物线y=ax2+bx+3经过A(-1,0),B(3,0)两点,
∴$\left\{\begin{array}{l}{a-b+3=0}\\{9a+3b+3=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$,
∴抛物线解析式为y=-x2+2x+3;
(2)∵y=-x2+2x+3=-(x-1)2+4,
∴顶点D的坐标为(1,4),
∵B(3,0),C(0,3),
∴BC2=(0-3)2+(3-0)2=18,
CD2=(1-0)2+(4-3)2=2,
BD2=(1-3)2+(4-0)2=20,
∴BC2+CD2=BD2,
∴△BCD是直角三角形,且∠BCD=90°,
∴tan∠DBC=$\frac{CD}{BC}$=$\frac{\sqrt{2}}{\sqrt{18}}$=$\frac{1}{3}$;
(3)如图,
∵A(-1,0),C(0,3),B(3,0),
∴直线AC的解析式为y=3x+3,直线BC的解析式为y=-x+3.
∵直线PE,AC交于点Q,
∴可设Q点坐标为(a,3a+3).
∵PQ⊥BC,
∴直线PQ的斜率为1,且直线PQ过点Q(a,3a+3),
∴直线PQ的解析式为y=x+2a+3,
∵AQ=GQ,A(-1,0),Q(a,3a+3),
∴点G纵坐标为6a+6,
∵点M是直线PE上的点,
∴点M坐标为(4a+3,6a+6),
∵点M是抛物线上点,
∴6a+6=-(4a+3)2+2(4a+3)+3,
解得:a=-$\frac{3}{8}$或a=1(不符合题意舍去),
∴点M坐标为($\frac{3}{2}$,$\frac{15}{4}$).
点评 本题是二次函数综合题,其中涉及到利用待定系数法求二次函数、一次函数的解析式,二次函数的性质,两点间的距离公式,勾股定理的逆定理,锐角三角函数定义,函数图象上点的坐标特征,互相垂直的两直线斜率之积为-1,一元二次方程的解法等知识,综合性较强,难度适中.利用数形结合、方程思想是解题的关键.

 阅读快车系列答案
阅读快车系列答案 如图,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是( )
如图,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是( )| A. | 25° | B. | 40° | C. | 50° | D. | 65° |
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
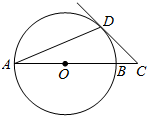 如图,AB是⊙O的直径,且AB=2$\sqrt{2}$,AD是弦,∠DAB=22.5°,延长AB到点C,使得∠ACD=45°,则BC的长是( )
如图,AB是⊙O的直径,且AB=2$\sqrt{2}$,AD是弦,∠DAB=22.5°,延长AB到点C,使得∠ACD=45°,则BC的长是( )| A. | 2$\sqrt{2}$-2 | B. | $\sqrt{2}$ | C. | 1 | D. | 2-$\sqrt{2}$ |
| A. | a2-6a+9 | B. | a2-3a+9 | C. | a2-9 | D. | a2-6a-9 |