题目内容
10．
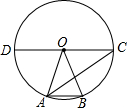如图，在⊙O中，A，B是圆上的两点，已知∠AOB=40°，直径CD∥AB，连接AC，则∠BAC=35度．
分析 先根据等腰三角形的性质求出∠ABO的度数，再由平行线的性质求出∠BOC的度数，根据圆周角定理即可得出结论．
解答 解：∵∠AOB=40°，OA=OB，
∴∠ABO=$\frac{180°-40°}{2}$=70°．
∵直径CD∥AB，
∴∠BOC=∠ABO=70°，
∴∠BAC=$\frac{1}{2}$∠BOC=35°．
故答案为：35．
点评 本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
20．
如图，点A、B、C都在⊙O上，若∠ACB=29°，则∠AOB的度数为（ ）
如图，点A、B、C都在⊙O上，若∠ACB=29°，则∠AOB的度数为（ ）| A． | 14.5° | B． | 29° | C． | 58° | D． | 61° |
解不等式2x-1＞$\frac{3x-1}{2}$，并把它的解集在数轴上表示出来．
如图，将△ABC沿直线DE折叠，使点C与点A重合，已知AB=7，BC=6，则△BCD的周长为13．
2．
如图，圆O是Rt△ABC的外接圆，∠ACB=90°，∠A=25°，过点C作圆O的切线，交AB的延长线于点D，则∠D的度数是（ ）
如图，圆O是Rt△ABC的外接圆，∠ACB=90°，∠A=25°，过点C作圆O的切线，交AB的延长线于点D，则∠D的度数是（ ）| A． | 25° | B． | 40° | C． | 50° | D． | 65° |
19．
三本相同的书本叠成如图所示的几何体，它的主视图是（ ）
三本相同的书本叠成如图所示的几何体，它的主视图是（ ）| A． |  | B． |  | C． |  | D． |  |