题目内容
13．
如图，直线a∥b，直线l与a、b分别相交于A、B两点，过点A作直线l的垂线交直线b于点C，若∠1=58°，则∠2的度数为（ ）| A． | 58° | B． | 42° | C． | 32° | D． | 28° |
分析 根据平行线的性质得出∠ACB=∠2，根据三角形内角和定理求出即可．
解答 解：∵直线a∥b，
∴∠ACB=∠2，
∵AC⊥BA，
∴∠BAC=90°，
∴∠2=∠ACB=180°-∠1-∠BAC=180°-90°-58°=32°，
故选C．
点评 本题考查了对平行线的性质和三角形内角和定理的应用，注意：①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
8．
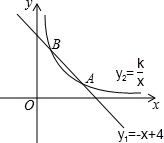如图，函数y1=-x+4的图象与函数y2=$\frac{k}{x}$（x＞0）的图象交于A（m，1），B（1，n）两点．
（1）求k，m，n的值；
（2）利用图象写出当x≥1时，y1和y2的大小关系．
如图，函数y1=-x+4的图象与函数y2=$\frac{k}{x}$（x＞0）的图象交于A（m，1），B（1，n）两点．（1）求k，m，n的值；
（2）利用图象写出当x≥1时，y1和y2的大小关系．
解不等式2x-1＞$\frac{3x-1}{2}$，并把它的解集在数轴上表示出来．
如图，将△ABC沿直线DE折叠，使点C与点A重合，已知AB=7，BC=6，则△BCD的周长为13．
2．
如图，圆O是Rt△ABC的外接圆，∠ACB=90°，∠A=25°，过点C作圆O的切线，交AB的延长线于点D，则∠D的度数是（ ）
如图，圆O是Rt△ABC的外接圆，∠ACB=90°，∠A=25°，过点C作圆O的切线，交AB的延长线于点D，则∠D的度数是（ ）| A． | 25° | B． | 40° | C． | 50° | D． | 65° |
3．一元二次方程2x2-3x+1=0的根的情况是（ ）
| A． | 有两个相等的实数根 | B． | 有两个不相等的实数根 | ||
| C． | 只有一个实数根 | D． | 没有实数根 |