题目内容
20. 如图所示,已知EF⊥AB,垂足为F,CD⊥AB,垂足为D,∠1=∠2,试判断∠AGD和∠ACB是否相等,为什么?(将解答过程补充完整)
如图所示,已知EF⊥AB,垂足为F,CD⊥AB,垂足为D,∠1=∠2,试判断∠AGD和∠ACB是否相等,为什么?(将解答过程补充完整)解:∠AGD=∠ACB.
理由如下:EF⊥AB,CD⊥AB(已知)
∴∠EFB=∠CDB=90° (垂直的定义)
∴CD∥EF (垂直于同一条直线的两条直线互相平行)
∴∠1=∠ECD(两直线平行,同位角相等)
又∠1=∠2(已知)
∴∠ECD=∠2( 等量代换 )
∴DG∥BC ( 内错角相等,两直线平行 )
∴∠AGD=∠ACB (两直线平行,同位角相等).
分析 先根据垂直的定义得出∠EFB=∠CDB=90°,故可得出CD∥EF,∠1=∠ECD,再由∠1=∠2可知∠ECD=∠2,故可得出DG∥BC,进而可得出结论.
解答 解:∠AGD=∠ACB.
理由如下:EF⊥AB,CD⊥AB(已知),
∴∠EFB=∠CDB=90° (垂直的定义),
∴CD∥EF (垂直于同一条直线的两条直线互相平行),
∴∠1=∠ECD(两直线平行,同位角相等).
又∵∠1=∠2(已知),
∴∠ECD=∠2( 等量代换 ),
∴DG∥BC( 内错角相等,两直线平行 ),
∴∠AGD=∠ACB (两直线平行,同位角相等).
故答案为:垂直的定义;垂直于同一条直线的两条直线互相平行;两直线平行,同位角相等;∠2;DG,BC;两直线平行,同位角相等.
点评 本题考查的是平行线的判定与性质,熟知平行线的判定定理是解答此题的关键.

练习册系列答案
相关题目
9.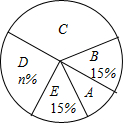 某校未为了解学生每天参加体育锻炼的时间情况,随机选取该校的部分学生进行调查.以下是根据调查结果绘制的统计图表的一部分.
某校未为了解学生每天参加体育锻炼的时间情况,随机选取该校的部分学生进行调查.以下是根据调查结果绘制的统计图表的一部分.
根据以上信息,解答下列问题:
(1)被调查的学生中,每天参加体育锻炼的时间不少于90min的有18人,这些学生数占被调查总人数的百分比为15%,每天参加体育锻炼的时间不足60min的有30人;
(2)被调查的学生总数为120人,统计表中m的值为42,统计图中n的值为25,被调查学生每天参加体育锻炼时间的中位数落在C组;
(3)该校共有960名学生,根据调查结果,估计该校每天参加体育锻炼的时间不少于60min的学生数.
 某校未为了解学生每天参加体育锻炼的时间情况,随机选取该校的部分学生进行调查.以下是根据调查结果绘制的统计图表的一部分.
某校未为了解学生每天参加体育锻炼的时间情况,随机选取该校的部分学生进行调查.以下是根据调查结果绘制的统计图表的一部分.| 组别 | A | B | C | D | E |
| 时间t/min | t<45 | 45≤t<60 | 60≤t<75 | 75≤t<90 | t≥90 |
| 人数 | 12 | 18 | m | 30 | 18 |
(1)被调查的学生中,每天参加体育锻炼的时间不少于90min的有18人,这些学生数占被调查总人数的百分比为15%,每天参加体育锻炼的时间不足60min的有30人;
(2)被调查的学生总数为120人,统计表中m的值为42,统计图中n的值为25,被调查学生每天参加体育锻炼时间的中位数落在C组;
(3)该校共有960名学生,根据调查结果,估计该校每天参加体育锻炼的时间不少于60min的学生数.
10.王华、张伟两位同学分别将自己10次数学自我检测的成绩绘制成如下统计图:
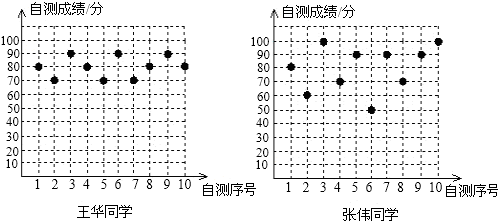
(1)根据图中提供的数据列出如下统计表:
则a=80,b=80,c=90,d=60,
(2)将90分以上(含90分)的成绩视为优秀,则优秀率高的是张伟.
(3)现在要从这两个同学选一位去参加数学竞赛,你可以根据以上的数据给老师哪些建议?

(1)根据图中提供的数据列出如下统计表:
| 平均成绩(分) | 中位数(分) | 众数(分) | 方差(S2) | |
| 王华 | 80 | b | 80 | d |
| 张伟 | a | 85 | c | 260 |
(2)将90分以上(含90分)的成绩视为优秀,则优秀率高的是张伟.
(3)现在要从这两个同学选一位去参加数学竞赛,你可以根据以上的数据给老师哪些建议?
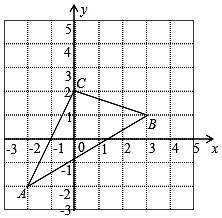 如图,△ABC在直角坐标系中
如图,△ABC在直角坐标系中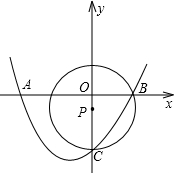 如图,抛物线y=ax2+bx+c(a≠0)经过x轴上的两点A(x1,0)、B(x2,0)和y轴上的点C(0,8),⊙P的圆心P在y轴上,且经过B、C两点,若b=2a,AB=6.
如图,抛物线y=ax2+bx+c(a≠0)经过x轴上的两点A(x1,0)、B(x2,0)和y轴上的点C(0,8),⊙P的圆心P在y轴上,且经过B、C两点,若b=2a,AB=6.