题目内容
4．
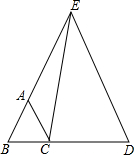已知BD=AE，AB=BC=CA，求证：EC=ED．
分析 首先延长BD至F，使DF=BC，连接EF，得出△BEF为等边三角形，进而求出△ECB≌△EDF，从而得出EC=DE．
解答 证明：延长BD至F，使DF=BC，连接EF，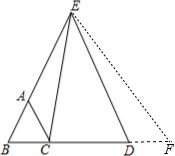
∵AE=BD，△ABC为等边三角形，
∴BE=BF，∠B=60°，
∴△BEF为等边三角形，
∴∠F=60°，
在△ECB和△EDF中
$\left\{\begin{array}{l}{BE=EF}\\{∠B=∠F=60°}\\{BC=DF}\end{array}\right.$
∴△ECB≌△EDF（SAS），
∴EC=ED．
点评 此题主要考查了等边三角形的性质与判定以及全等三角形的判定等知识，作出辅助线是解决问题的关键．
练习册系列答案
相关题目
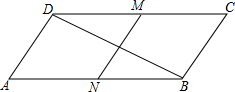已知：平行四边形ABCD，AB=2AD，∠A=60°，M，N分别是DC，AB中点．求证：MN⊥DB．
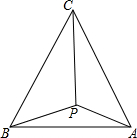如图所示，P是正三角形ABC内一点，PA=2，PB=2$\sqrt{3}$，PC=4，求BC的长．
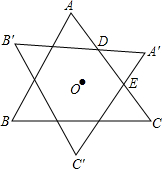如图，将等边三角形ABC绕其外心O顺时针旋转α（0°＜α＜120°）至△A′B′C′，交AC于点D，E，若以AD，DE，EC为三边所围成的三角形为直角三角形，则旋转角α=30°或90°．